OpenGLでは用意されている座標変換のための関数が、WebGLでは用意されて いないので自前で用意するか、誰かの作成したライブラリを利用する必要があります。 ここでは、教科書に付属している cuon-matrix.js を使うことにします。 このライブラリでは Matrix4 というjavascriptのオブジェクトが定義されています。
Matrix4では、乗算は右方向から行うことに注意して下さい。
| Matrix4のプロパティ |
|---|
elements 行列の要素を保持する型付き配列(Float32Array) |
| Matrix4のメソッド |
setIdentity() 単位行列に設定する。 @return this |
set(src) 渡された行列の要素をコピーする。 @param src 要素をコピーしてくる行列 @return this |
multiply(other) 渡された行列を右からかける。 @param other かける行列 @return this |
multiplyVector3(pos) 渡されたベクトルをかける。 @param pos かける行列 @return この行列を掛けた結果(Float32Array) |
multiplyVector4(pos) 渡されたベクトルをかける。 @param pos かける行列 @return この行列を掛けた結果(Float32Array) |
transpose() 行列を転置する。 @return this |
invert() この行列の逆行列を計算して、内容を置き換える。 @return this |
ortho(left, right, bottom, top, near, far) 正射影行列を右からかける。 @param left 左クリップ平面のX座標 @param right 右クリップ平面のX座標 @param bottom 下クリップ平面のY座標 @param top 上クリップ平面のY座標 @param near 近クリップ平面までの距離。平面が視点の後方にある場合は負数 @param far 遠クリップ平面までの距離。平面が視点の後方にある場合は負数 @return this |
frustum(left, right, bottom, top, near, far) 透視射影行列を右からかける。 @param left 近クリップ平面上における左クリップ平面のX座標 @param right 近クリップ平面上における右クリップ平面のX座標 @param bottom 近クリップ平面上における下クリップ平面のY座標 @param top 近クリップ平面上における上クリップ平面のY座標 @param near 近クリップ平面までの距離。正数でなくてはならない @param far 遠クリップ平面までの距離。正数でなくてはならない @return this |
perspective(fovy, aspect, near, far) 透視射影行列を右からかける。 @param fovy 垂直視野角 [度] @param aspect 視野のアスペクト比(幅 / 高さ) @param near 近クリップ平面までの距離。正数でなくてはならない @param far 遠クリップ平面までの距離。正数でなくてはならない @return this |
scale(x, y, z) * スケーリング行列を右からかける。 * @param x X方向の倍率 * @param y Y方向の倍率 * @param z Z方向の倍率 * @return this |
translate(x, y, z) 平行移動行列を右からかける。 @param x X方向の移動量 @param y Y方向の移動量 @param z Z方向の移動量 @return this |
rotate(angle, x, y, z) 回転行列を右からかける。 回転軸の方向ベクトルは正規化されていなくても構わない。 @param angle 回転角 [度] @param x 回転軸の方向ベクトルのX成分 @param y 回転軸の方向ベクトルのY成分 @param z 回転軸の方向ベクトルのZ成分 @return this |
lookAt(eyeX, eyeY, eyeZ, centerX, centerY, centerZ, upX, upY, upZ) 視野変換行列を右からかける。 @param eyeX, eyeY, eyeZ 視点の位置 @param centerX, centerY, centerZ 注視点の位置 @param upX, upY, upZ カメラの上方向を表す方向ベクトル @return this |
dropShadow(plane, light) 頂点を平面上に射影するような行列を右からかける。 @param plane 平面方程式 Ax + By + Cz + D = 0 の係数[A, B, C, D]を格納した配列 @param light 光源の同次座標を格納した配列。light[3]=0の場合、平行光源を表す @return this |
dropShadowDirectionally(normX, normY, normZ, planeX, planeY, planeZ, lightX, lightY, lightZ) 平行光源により頂点を平面上に射影するような行列を右からかける。 @param normX, normY, normZ 平面の法線ベクトル(正規化されている必要はない) @param planeX, planeY, planeZ 平面上の点 @param lightX, lightY, lightZ ライトの方向(正規化されている必要はない) @return this |
3次元座標系 y | | /---------x / / z
頂点シェーダの中で、頂点の座標に対して変換行列をかけるようにしましょう。 モデル変換行列、ビュー変換行列、透視投影変換行列をこの順に右からかけた 結果が u_MvpMatrixです。

モデル行列で、y軸回りに-10度回転させると次のようになります。

図形を座標配列のインデックスの集合で表現することができます。
その場合は、頂点の座標を頂点シェーダの attribute 変数を 経由して gl_Position に設定した上で、 図形を表すインデックスの配列をバッファオブジェクトとして WebGLのELEMENT_ARRAY_BUFFERをターゲットとして送り込んでおき、 gl.drawElements()を使って描画します。
インデックスの配列のバッファオブジェクトをjavascriptからWebGLに転送した後、 一旦はELEMENT_ARRAY_BUFFERとバッファオブジェクトのバインドを解消しても 構いませんが、g.drawElements()で描画する時点では再びバインドしておく 必要があります。

下の例では、9個の頂点座標を使って、12個のインデックスを与え、 gl.TRIANGLESで描いているので合計4個の3角形が描画されています。
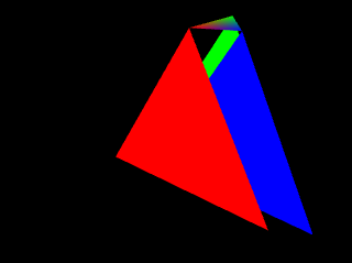
底面が一辺の長さが2の正方形で高さが2の四角錐を表示するのが LookAtPyramidElement.htmlです。
頂点の座標 色 P0:( 0, 2, 0) (1,1,1) P1:( 1, 0, 1) (1,0,0) P2:( 1, 0,-1) (0,1,0) P3:(-1, 0,-1) (0,0,1) P4:(-1, 0, 1) (0.5,0.5,0) 視点:(6.0, -2.0, 4.0), 注視点:(0.0, 0.0, 0.0), 上方向:(0.0, 1.0, 0.0)

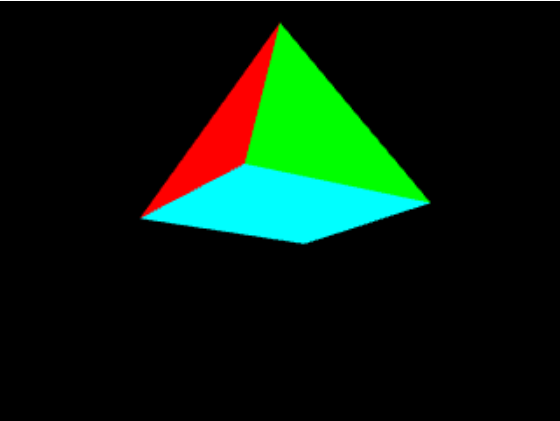
前の例だと頂点が複数の面(三角形)で共有されているため、 面ごとに色を変えようとしても混ざってしまっています。 そのような場合は、頂点が別の面に属する場合は、 同じ位置にある別の頂点と考えて定義します。
次回以降で面の法線の計算を行うため、必ず次の条件を満たすように 頂点のインデックスを記述して下さい。
三角形を表す3個のindexがi, (i+1), (i+2)であり、 それぞれのインデックスが表す頂点の座標を Pi , Pi+1 , Pi+2 とするとき、
モデル行列として「y軸回りに45度回転してから、x軸方向に-3平行移動する」という行列を設定してから MvpMatrixを再計算し、uniform変数 u_MvpMatrix 経由で WebGL に送りこんで描画させてみます。 前の描画を消さずに次の図形を描画したので、合計で2個の図形が描画されています。 あとから描いた図形が、先に描いた図形の後ろに正しく描画されていることに注意して下さい。

モデル行列の内容を変更しながら、 画面を消しては再描画することを繰り返すとアニメーションになります。
setIntevalの第1引数で指定する関数は、Globalスコープ (Globalオブジェクト)からアクセスできる 状態でなければいけないことに注意して下さい。

元は同じ形ですが、1.5倍したものを (-4, 0, 0) だけ平行移動して後ろに表示してみます。 手前の物体はy軸回りに、奥の物体はx軸回りに回転しています。
