逆転置行列

ある平面 $P$ とその法線ベクトル $\vec n$ が与えられている。平面 $\rm P$ が行列 $M$ によって座標変換を受けて平面 $\rm P'$ になったとき、 $P'$ に垂直な法線 $\vec {n'}$ を求めたい。

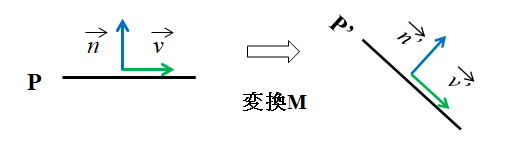
平面 $\rm P$ および平面 $\rm P'$ 内のベクトルをそれぞれ $\vec v$ , $\vec {v'}$ とすると、 $$\vec {v'} = M \vec v \quad ... (\dagger 1)$$ であり、また、$\vec n \bot \vec v$ および $\vec {n'} \bot \vec {v'}$ より $$ \vec n \cdot \vec v = 0 \quad ... (\dagger 2) \\ \vec {n'} \cdot \vec {v'} = 0 \quad ... (\dagger 3) $$ が成り立つ。ここで、 $$\vec {n'}= A \vec n \quad ...(\dagger 4)$$ となる行列 $A$ が存在したとすると $(\dagger 1)$ と$ (\dagger 4)$ を $(\dagger 3)$ の式に代入して $$(A \vec n) \cdot (M \vec v) = 0 \\ \vec n \cdot (A^{\rm T} M \vec v) = 0 $$ ここで $(\dagger 2)$ がなりたつので、 $A^{\rm T} M = E$となるように $A$ を選べばよいことがわかる。 $$ A^{\rm T} M = E \\ A^{\rm T} = M^{-1} \\ A = (M^{-1})^{\rm T} $$

転置行列

wikipediaより。

転置行列 (てんちぎょうれつ、transposed matrix)とは $m$ 行 $n$ 列の行列 $A$ に対して $A$ の ($i$, $j$) 要素と ($j$, $i$) 要素を入れ替えた $n$ 行 $m$ 列の行列、つまり対角線で成分を折り返した行列のことである。転置行列は $A^{\rm T}$ や ${}^{\rm t}A$、また $A^{\rm tr}$ などと表現される。

例 \[ A = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix},\quad B = \begin{pmatrix} a & b & c \\ d & e & f \end{pmatrix}, \quad C = \begin{pmatrix} g & h & i \end{pmatrix} \] に対して転置行列 $A^{\rm T}$, $B^{\rm T}$, $C^{\rm T}$ はそれぞれ \[ A^{\rm T} = \begin{pmatrix} 1 & 4 & 7 \\ 2 & 5 & 8 \\ 3 & 6 & 9 \end{pmatrix}, \quad B^{\rm T} = \begin{pmatrix} a & d \\ b & e \\ c & f \end{pmatrix} \quad C^{\rm T} = \begin{pmatrix} g \\ h \\ i \end{pmatrix} . \]

性質

$A$, $B$ は行列、$k$ はスカラーとして次が成り立つ：
$(A^{\rm T})^{\rm T} = A \tag{1}$
$(A + B)^{\rm T} = A^{\rm T} + B^{\rm T} \tag{2} $
$(kA)^{\rm T} = k A^{\rm T} \tag{3}$
$(AB)^{\rm T} = B^{\rm T} A^{\rm T} \tag{4}$
$A$ は$n$ 次正方行列、$x$, $y$は$n$ 次元ベクトルとすると内積 $\cdot$ に対して次が成り立つ。 $(Ax) \cdot y = x \cdot (A^{\rm T}y) \tag{5}$

証明

(1)〜(3)は自明。

(4)の証明は以下の通り。

$A$を$m\times n$行列、$B$を$n\times r$行列とする。 \[ A = \begin{pmatrix} a_{11} & \cdots & a_{1j} & \cdots & a_{1n} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ a_{i1} & \cdots & a_{ij} & \cdots & a_{in} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ a_{m1} & \cdots & a_{mj} & \cdots & a_{mn} \\ \end{pmatrix},\quad B = \begin{pmatrix} b_{11} & \cdots & b_{1j} & \cdots & b_{1r} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ b_{i1} & \cdots & b_{ij} & \cdots & b_{ir} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ b_{n1} & \cdots & b_{nj} & \cdots & b_{nr} \\ \end{pmatrix} \] に対して $AB$の($i$, $j$)成分は$A$の$i$行と$B$の$j$行の積であり \[ \begin{pmatrix} a_{i1} & \cdots & a_{ij} & \cdots & a_{in} \\ \end{pmatrix} \begin{pmatrix} b_{1j} \\ \vdots \\ b_{ij} \\ \vdots \\ b_{nj} \\ \end{pmatrix} = \displaystyle \sum^{n}_{k=1}a_{ik}b_{kj} \tag{*1} \] である。これが $(AB)^{\rm T}$ の($j$, $i$)成分となる。一方, \[ B^{\rm T} = \begin{pmatrix} b_{11} & \cdots & b_{i1} & \cdots & b_{n1} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ b_{1j} & \cdots & b_{ij} & \cdots & b_{nj} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ b_{1r} & \cdots & b_{ir} & \cdots & b_{nr} \\ \end{pmatrix}, \quad A^{\rm T} = \begin{pmatrix} a_{11} & \cdots & a_{i1} & \cdots & a_{m1} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ a_{1j} & \cdots & a_{ij} & \cdots & a_{mj} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ a_{1n} & \cdots & a_{in} & \cdots & a_{mn} \\ \end{pmatrix} \] として $B^{\rm T} A^{\rm T}$の($j$, $i$)成分は、 \[ \begin{pmatrix} b_{1j} & \cdots & b_{ij} & \cdots & b_{nj} \tag{*2}\\ \end{pmatrix} \begin{pmatrix} a_{i1} \\ \vdots \\ a_{ij} \\ \vdots \\ a_{in} \\ \end{pmatrix} = \displaystyle \sum^{n}_{k=1} b_{kj} a_{ik} = \sum^{n}_{k=1} a_{ik} b_{kj} \] となり、$(*1)$と$(*2)$が等しいので $(AB)^{\rm T} = B^{\rm T} A^{\rm T}$ が証明された。

(5)の証明は以下の通り。

$A$を$n\times n$行列、$x$, $y$ を$n$次元ベクトルとする。 \[ A = \begin{pmatrix} a_{11} & \cdots & a_{1j} & \cdots & a_{1n} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ a_{i1} & \cdots & a_{ij} & \cdots & a_{in} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ a_{n1} & \cdots & a_{nj} & \cdots & a_{nn} \\ \end{pmatrix},\quad x = \begin{pmatrix} x_{1} \\ \vdots \\ x_{i} \\ \vdots \\ x_{n} \\ \end{pmatrix},\quad y = \begin{pmatrix} y_{1} \\ \vdots \\ y_{i} \\ \vdots \\ y_{n} \\ \end{pmatrix} \] とすると、
$\begin{eqnarray} (Ax) \cdot y & = & ( \begin{pmatrix} a_{11} & \cdots & a_{1j} & \cdots & a_{1n} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ a_{i1} & \cdots & a_{ij} & \cdots & a_{in} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ a_{n1} & \cdots & a_{nj} & \cdots & a_{nn} \\ \end{pmatrix} \begin{pmatrix} x_{1} \\ \vdots \\ x_{i} \\ \vdots \\ x_{n} \\ \end{pmatrix} ) \cdot \begin{pmatrix} y_{1} \\ \vdots \\ y_{i} \\ \vdots \\ y_{n} \\ \end{pmatrix} \\ &=& \begin{pmatrix} a_{11} x_1 + \cdots + a_{1j} x_j + \cdots + a_{1n} x_n \\ \vdots \\ a_{i1} x_1 + \cdots + a_{ij} x_j + \cdots + a_{in} x_n \\ \vdots \\ a_{n1} x_1 + \cdots + a_{nj} x_j + \cdots + a_{nn} x_n \\ \end{pmatrix} \cdot \begin{pmatrix} y_{1} \\ \vdots \\ y_{i} \\ \vdots \\ y_{n} \\ \end{pmatrix} \\ & = & (a_{11} x_1 + \cdots + a_{1j} x_j + \cdots + a_{1n} x_n ) y_1 + \cdots + (a_{i1} x_1 + \cdots + a_{ij} x_j + \cdots + a_{in} x_n ) y_i + \\ & & \cdots + (a_{n1} x_1 + \cdots + a_{nj} x_j + \cdots + a_{nn} x_n ) y_n \\ & = & x_1 (a_{11} y_1 + \cdots + a_{i1} y_i + ... + a_{n1} y_n) + \cdots + x_j (a_{1j} y_1 + \cdots + a_{ij} y_i + ... + a_{nj} y_n) + \\ & & \cdots + x_n (a_{1n} y_1 + \cdots + a_{in} y_n + ... + a_{nn} y_n) \\ & =& \begin{pmatrix} x_1 \\ \vdots \\ x_j \\ \vdots \\ x_n \\ \end{pmatrix} \cdot \begin{pmatrix} a_{11} y_1 + \cdots + a_{i1} y_i + ... + a_{n1} y_n \\ \vdots \\ a_{1j} y_1 + \cdots + a_{ij} y_i + ... + a_{nj} y_n \\ \vdots \\ a_{1n} y_1 + \cdots + a_{in} y_n + ... + a_{nn} y_n \\ \end{pmatrix} \\ & =& \begin{pmatrix} x_1 \\ \vdots \\ x_j \\ \vdots \\ x_n \\ \end{pmatrix} \cdot ( \begin{pmatrix} a_{11} & \cdots & a_{i1} & \cdots & a_{m1} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ a_{1j} & \cdots & a_{ij} & \cdots & a_{mj} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ a_{1n} & \cdots & a_{in} & \cdots & a_{mn} \\ \end{pmatrix} \begin{pmatrix} y_{1} \\ \vdots \\ y_{j} \\ \vdots \\ y_{n} \\ \end{pmatrix} ) \quad = x \cdot (A^{\rm T} y) \end{eqnarray}$