コンピュータグラフィックス 第4回
レンダリング(1)
数学的基礎
ベクトルの内積(dot product) と外積(cross product)
ベクトル
$ \overrightarrow{v_1} = \begin{pmatrix}x_1 \\ y_1 \\ z_1 \end{pmatrix} $
,
$ \overrightarrow{v_2} = \begin{pmatrix}x_2 \\ y_2 \\ z_2 \end{pmatrix} $
のなす角を$\theta$とすると、
内積
$ \overrightarrow{v_1} \cdot \overrightarrow{v_1}
= x_1 x_2 + y_1 y_2 + z_1 z_2 = |\overrightarrow{v_1}| |\overrightarrow{v_2}| \cos\theta
$
,
外積
$ \overrightarrow{v_1} \times \overrightarrow{v_1}
= \begin{pmatrix} y_1 z_2 - z_1 y_2 \\ z_1 x2 - x_1 z_2 \\ x_1 y2 - y_1 x_2 \end{pmatrix}
\equiv \overrightarrow{v_3}
$
$\quad\quad\quad$計算方法 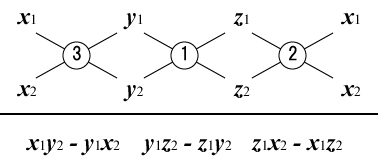
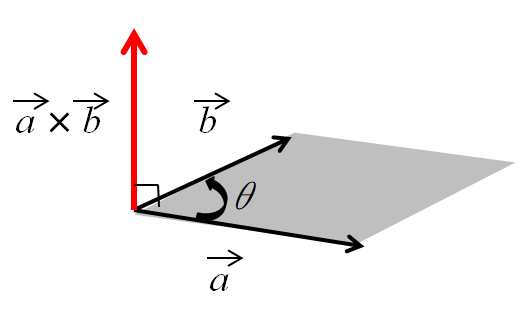
$\overrightarrow{v_3} $ は「
$\overrightarrow{v_1}$ が $\overrightarrow{v_2}$ の方向を向くように回転させたとき右ねじが進む方向 」
のベクトルであり、大きさは「$\overrightarrow{v_1}$ と $\overrightarrow{v_2}$が作る平行四辺形」の面積と等しい。
$|\overrightarrow{v_3}| = |\overrightarrow{v_1}| |\overrightarrow{v_2}| \sin\theta $
$\overrightarrow{v_3} \cdot \overrightarrow{v_1} = 0 \quad , \quad \quad
\overrightarrow{v_3} \cdot \overrightarrow{v_2} = 0 $
証明
$\displaystyle
\begin{eqnarray}
\overrightarrow{v_3} \cdot \overrightarrow{v_1} & = & (y_1 z_2 - z_1 y_2)x_1 + (z_1 x_2 - x_1 z_2) y_1 + (x_1 y_2 - y_1 x_2) z_1 \\
& = & x_1 y_1 z_2 - x_1 y_2 z_1 + x_2y_1z_1 - x_1y_1z_2 + x_1y_2z_1 - y_1x_2z_1 \\
& = & 0 \\
\overrightarrow{v_3} \cdot \overrightarrow{v_2} & = & (y_1 z_2 - z_1 y_2)x_2 + (z_1 x_2 - x_1 z_2) y_2 + (x_1 y_2 - y_1 x_2) z_2 \\
& = & x_2 y_1 z_2 - x_2 y_2 z_1 + x_2 y_2 z_1 - x_1 y_2 z_2 + x_1 y_2 z_2 - x_2 y_1 z_2 \\
& = & 0 \\
\end{eqnarray}
$
$|\overrightarrow{v_3}| = |\overrightarrow{v_1}| |\overrightarrow{v_2}| \sin\theta $ を証明する。
ベクトル
$ \overrightarrow{v_1} = \begin{pmatrix}x_1 \\ y_1 \\ 0 \end{pmatrix} $
,
$ \overrightarrow{v_2} = \begin{pmatrix}x_2 \\ y_2 \\ 0 \end{pmatrix} $
とおいても一般性能は失われない。このとき
$ \overrightarrow{v_3} = \begin{pmatrix}0 \\ 0 \\ x_1 y_2 - x_2 y_1 \end{pmatrix} $
$ \overrightarrow{v_1}$ と
$ \overrightarrow{v_2}$ のなす角を $\theta$ とすると、
$\displaystyle
\begin{eqnarray}
|\overrightarrow{v_1}| |\overrightarrow{v_2}| \sin \theta & = & |\overrightarrow{v_1}| |\overrightarrow{v_2}| \sqrt{1-\cos^2 \theta} \\
& = & |\overrightarrow{v_1}| |\overrightarrow{v_2}| \sqrt{1- \left( \frac{\overrightarrow{v_1} \cdot \overrightarrow{v_2}}{|\overrightarrow{v_1}| |\overrightarrow{v_2}|} \right)^2 } \\
& = & \sqrt{|\overrightarrow{v_1}|^2 |\overrightarrow{v_2}|^2 - (\overrightarrow{v_1} \cdot \overrightarrow{v_2})^2} \\
& = & \sqrt{(x_1^2 + y_1^2)(x_2^2+y_2^2) - (x_1 x_2 + y_1 y_2)^2} \\
& = & \sqrt{x_1^2 x_2^2 + x_1^2 y_2^2 + y_1^2 x_2^2 + y_1^2 y_2^2 - (x_1^2 x_2^2 + 2 x_1 x_2 y_1 y_2 + y_1^2 y_2^2)} \\
& = & \sqrt{x_1^2 y_2^2 - 2 x_1 x_2 y_1 y_2 + y_1^2 x_2^2} \\
& = & \sqrt{ (x_1 y_2 - y_1 x_2)^2} \\
& = & |x_1 y_2 - y_1 x_2| \\
& = & |\overrightarrow{v_3}|
\end{eqnarray}
$
概要
「レンダリング」とは
「コンピュータ内部に記述された形状データから2次元デジタル画像を生成する処理」
のことである。光の物理的な性質に基づいて描画を行うことで写実的な画像を生成できる。
写実表現のレベル
3次元物体を2次元画像として表示する。
カメラで実際の物体を撮影したときに得られるような
写実的な画像を生成するフォトリアリスティックレンダリング手法が開発されてきた。
- ワイヤーフレーム(線画),デプスキューイング(遠くの線の輝度を落とす), 隠線消去 (見えない線の消去)
- 隠面消去&シェーディング(陰影づけ)、影つけ、テクスチャ(物体表面の模様)の付加

リアリティの要素
- 遠近感
- 可視面の表示
- 陰影と影つけ
- 物体の材質
- 表面の滑らかさ
- 反射光の計算
- スムーズシェーディング(滑らかな陰影つけ)
- バンプマッピング(表面の微細な凹凸の表現)
- テクスチャマッピング (表面の詳細な模様の表現)
写実的表現のためのモデリング
3次元モデルの幾何学的形状だけでなく、物体の材質や
表面の滑らかさなどの物理的な属性も重要である。
複雑なシーンについてリアルな画像を生成するには、適切なモデリングと
レンダリング手法を組み合わせることが必要となる。
- 物体表面の反射率、RGBごとの反射率、拡散反射率、鏡面反射率
- 金属表面や透明物を表示する場合には、表面の粗さ係数や屈折率が必要となる。
- 物体表面の反射特性である BRDF (双方向反射分布関数) を使うと、より一般化された反射を扱うことができる。
レンダリングを構成する処理

陰面消去
バックフェースカリング
バックフェースカリング (back-face culling) は、陰面消去の前処理で、
視点から不可視となる裏面を除去する処理のことである。
面の法線ベクトル $\vec{N}$ と視線方向ベクトル $\vec{V}$ のなす角度が、鋭角のときは可視(表面)、
鈍角のときは不可視(裏面)と判断する。
ベクトルの内積 $\vec{V}\cdot\vec{N}$ で計算できる。
$\vec{V}\cdot\vec{N} = |\vec{V}| |\vec{N}| \cos \theta$


視線方向ベクトルと法線ベクトル
視線方向ベクトル V は、面を構成する任意の頂点
$\vec{P_i}$
から視点
$\vec{P_E}$
へのベクトルなので
$\vec{V} = \overrightarrow{P_i P_E} = \vec{P_E} - \vec{P_i}$ となる。
物体を構成する凸ポリゴンの頂点は、物体を外側から見て反時計回りに番号付けされているものとする。
ポリゴンの任意の3頂点を$P_i$, $P_j$, $P_k$ (ただし$i \lt j \lt k$)を用いて、
法線ベクトル $\vec{N}$ は次の式で計算できる。
$\vec{N} = \overrightarrow{P_j P_i} \times \overrightarrow{P_k P_j}
= \overrightarrow{P_i P_j} \times \overrightarrow{P_j P_k}$
2つのベクトルの外積とはつぎのような計算である。
$
(x_0,y_0, z_0) \times
(x_1,y_1, z_1)
=
(
y_0 * z_1 - y_1 * z_0
,
z_0 * x_1 - z_ 1 * x_ 0
,
x_0 * y_1 - x_1 * y_0
)
$
隠面消去法
- 物体空間アルゴリズム (object space algorithm) --- 3次元で陰面消去の判定を直接行う方法
- 画像空間アルゴリズム (image space algorithm) --- 物体が投影されるスクリーン状のスキャンラインやピクセル単位で陰面消去の処理を行う方法(スキャンライン法、Zバッファ法、レイトレーシング法)
- 優先順位アルゴリズム (priority algorithm) --- 面の可視性の優先順位に基づいて陰面消去を行う方法
優先順位アルゴリズム
フレームバッファに対して、奥にある面を先に、手前にある面を後に描画する方法。
奥行きソート法 (depth-sort algorithm) は可視性の優先順位にしたがって面をソートし、可視性の低い遠方の面から順に描く方法。
面の優先順位が決定するのが難しい場合があり、ポリゴンや空間を分割するなどの
手法が必要となる。




スキャンライン法
スキャンライン (走査線, scanline)に基づいて隠面消去を行う方法であり、ポリゴンの
操作変換(scan conversion)を複数の重なりあったポリゴンでも処理できるように
拡張したもの。



「ポリゴンの走査変換」では、ポリゴンの辺とスキャンラインの交点を求めて、
ポリゴンに含まれる画素を決定する。
ポリゴンと交差する全てのスキャンラインについてこの処理を行い、
ポリゴン内部の点を塗りつぶすことにより、ベクトル表現されていたポリゴンを
ラスタ化(画像を色のついた点の集まりとして表現すること)できる。
スキャンラインとポリゴンの辺との交点を求めるには、一般には乗算や除算が
必要になるが、増分法(incrimental methods)を用いて加算のみで交点を算出できる。


スキャンライン法の特徴
- 他の方法に比べて使用するメモリ量が少ない。
「スキャンライン1本分のスキャンセグメント両端点のx座標値を配列に記憶する」
だけでよいので。
- 計算量も比較的少ない。走査平面と交差するポリゴンの選別や
サンプルスパンごとの可視部分の決定にコヒーレンス(平面内の点の連続性)が
使えるので。
- 主としてポリゴンによって構成された物体の表示に用いられ、
反射や屈折を扱うことはできない。
Zバッファ法
Zバッファ法 (Z-buffer algorithm) は、画素ごとに奥行きの判定を行い
隠面消去を行う方法。
フレームバッファ (画像の画素の色を格納する)と同じ解像度の
Zバッファ (奥行きであるz座標を格納する。デプスバッファとも言う)
を設ける。



ポリゴンの奥行き(z値)の計算
- ポリゴンの法線ベクトル
$\vec{N} =(n_x, n_y, n_z)$ 、
ポリゴンのいずれかの頂点を
$\vec{P_i} = (x_i, y_i,z_i)$,
ポリゴンを含む平面上の点を
$\vec{P} = (x,y,z)$
とすると、
$\overrightarrow{P_i P} \cdot \vec{N} = 0$
これを成分で表すと
$n_x x + n_y y + n_z z - (n_x x_i + n_y y_i + n_z z_i) = 0$
。
-
$z = (-n_x x - n_y y + n_x x_i + n_y y_i +n_z z_i) / n_z$
すなわち、$x$が1だけ変化すると$z$は$-n_x / n_z$変化するだけなので、単なる加算で計算できる。
Zバッファ法の特徴
- Zバッファ用のメモリが必要となる。
- アルゴリズムが比較的簡単でハードウェア化しやすい。
-
メモリ価格の低下により、PC用の3次元グラフィックスハードウェア
GPUではZバッファ法が採用されている。
レイトレーシング法
レイトレーシング法 (ray tracing algorithm、光線追跡法)は、
レイという1次元線分上での交点の前後判定により隠面消去を行う。





レイトレーシング法の特徴
- 直線との交差判定なので、レイと物体との交点を計算したり可視点を決定するのが
他の隠面消去アルゴリズムよりも単純であり、必要となるメモリも少ない。
- 直線との交点を求めることができる物体であれば、ポリゴン以外の
球や円錐など関数表現された物体も扱うことができる。
- 反射、透過、屈折など複雑な光学現象をリアルに表現することができる。
- 画素毎に処理を行うため、一般的に多くの計算時間を必要とする。
バウンディングボリュームやボクセル空間分割を用いて高速化する方法や、
複数のCPUで並列化する方法が開発されている。