コンピュータグラフィックス:理論(1)
座標変換
基礎知識
行列の乗算
2次元平面上の点($x$, $y$)が
$
\begin{equation}
\left \{
\begin{array}{l}
x' = ax + by \\
y' = cx + dy
\end{array}
\right. \quad\cdots (1)
\end{equation}
$
という線形変換によって($x'$, $y'$)に移動し、さらにこの($x'$, $y'$)が別の線形変換
$
\begin{equation}
\left \{
\begin{array}{l}
x'' = ex' + fy' \\
y'' = gx' + hy'
\end{array}
\right. \quad\cdots (2)
\end{equation}
$
によって($x''$, $y''$)に移動したとする。
式$(2)$の中の($x'$,$y'$)を式$(1)$を使って表すと、次の式が成り立つことがわかる。
$
\begin{equation}
\left \{
\begin{array}{l}
x'' = ex' + fy' = e(ax+by)+f(cx+dy) = (ea+fc)x + (eb+fd)y \\
y'' = gx' + hy' = f(ax+by)+h(cx+dy) = (ga+hc)x + (gb+hd)y
\end{array}
\right. \quad\cdots (3)
\end{equation}
$
ここで$(1)$の式を次のように表記することにしよう。(これが「行列 (Matrix)」による表現です。)
$
\begin{pmatrix}x' \\ y' \end{pmatrix}
= \begin{pmatrix}
ax+by \\
cx+dy \\
\end{pmatrix}
= \begin{pmatrix}
a & b \\
c & d \\
\end{pmatrix}
\begin{pmatrix}x \\ y \end{pmatrix} \quad\cdots (1')
$
すると、$(2)$, $(3)$はそれぞれ次のように記述できる。
$
\begin{pmatrix}x'' \\ y'' \end{pmatrix}
= \begin{pmatrix}
e & f \\
g & h \\
\end{pmatrix}
\begin{pmatrix}x' \\ y' \end{pmatrix} \quad\cdots (2')
$
$
\begin{pmatrix}x'' \\ y'' \end{pmatrix}
= \begin{pmatrix}
ea+fc & eb+fd \\
ga+hc & gb+hd \\
\end{pmatrix}
\begin{pmatrix}x \\ y \end{pmatrix} \quad\cdots (3')
$
$(2')$の中の($x'$, $y'$)の記述を、$(1')$を使って表すと次のようになる。
$
\begin{pmatrix}x'' \\ y'' \end{pmatrix}
= \begin{pmatrix}
e & f \\
g & g \\
\end{pmatrix}
\begin{pmatrix}
a & b \\
c & d \\
\end{pmatrix}
\begin{pmatrix}x \\ y \end{pmatrix} \quad\cdots (4)
$
$(3')$と$(4)$は等しいから、次の関係がいえる。(「行列の掛け算」を定義したことになります。)
$
\begin{pmatrix}
e & f \\
g & g \\
\end{pmatrix}
\begin{pmatrix}
a & b \\
c & d \\
\end{pmatrix}
= \begin{pmatrix}
ea+fc & eb+fd \\
ga+hc & gb+hd \\
\end{pmatrix}
$
2次元での回転
点 $\begin{pmatrix}x \\ y \end{pmatrix}$を原点回りに反時計方向$\theta$だけ回転した点を
$\begin{pmatrix}x' \\ y' \end{pmatrix}$
とおく。
$x$軸方向の単位ベクトル $\overrightarrow{e_x}$,
$y$軸方向の単位ベクトル $\overrightarrow{e_y}$
をそれぞれ原点回りに$\theta$だけ回転したベクトルを $\overrightarrow{e'_x}$, $\overrightarrow{e'_y}$,とする。
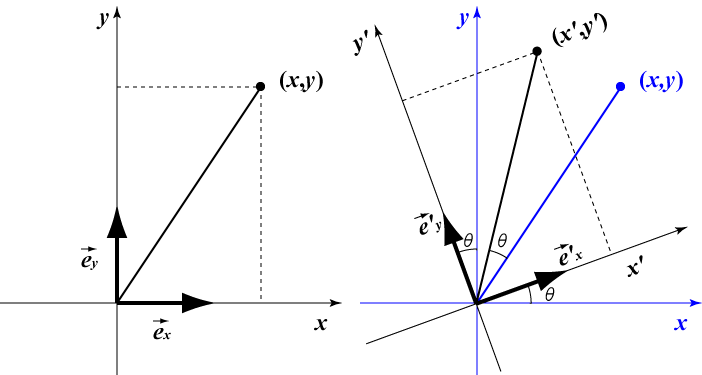
$\overrightarrow{e_x} = \begin{pmatrix}1 \\ 0 \end{pmatrix}$
$\quad\quad\quad\quad$
$\overrightarrow{e_y} = \begin{pmatrix}0 \\ 1 \end{pmatrix}$
$\quad\quad\quad\quad$
$\overrightarrow{e'_x} = \begin{pmatrix} \cos \theta \\ \sin \theta \end{pmatrix}$
$\quad\quad\quad\quad$
$\overrightarrow{e'_y} = \begin{pmatrix} -\sin \theta \\ \cos \theta \end{pmatrix}$
$
\begin{pmatrix}x \\ y \end{pmatrix}
= x \overrightarrow{e_x} + y \overrightarrow{e_y}
=
x
\begin{pmatrix}1 \\ 0 \end{pmatrix}
+
y
\begin{pmatrix}0 \\ 1 \end{pmatrix}
$
$
\begin{pmatrix}x' \\ y' \end{pmatrix}
= x \overrightarrow{e'_x} + y \overrightarrow{e'_y}
=
x
\begin{pmatrix} \cos\theta \\ \sin\theta \end{pmatrix}
+
y
\begin{pmatrix}-\sin\theta \\ \cos\theta \end{pmatrix}
=
\begin{pmatrix} x\cos\theta -y\sin\theta \\ x\sin\theta +y\cos\theta \end{pmatrix}
= \begin{pmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta \\
\end{pmatrix}
\begin{pmatrix}x \\ y \end{pmatrix}
$
3次元での回転
 $
\begin{pmatrix}x' \\ y' \end{pmatrix}
= \begin{pmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta \\
\end{pmatrix}
\begin{pmatrix}x \\ y \end{pmatrix}
\quad\quad\quad
\begin{pmatrix}x' \\ y' \\ z' \\ 1 \end{pmatrix}
= \begin{pmatrix}
\cos\theta & -\sin\theta & 0 & 0 \\
\sin\theta & \cos\theta & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}x \\ y \\ z \\ 1 \end{pmatrix}
$
$
\begin{pmatrix}x' \\ y' \end{pmatrix}
= \begin{pmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta \\
\end{pmatrix}
\begin{pmatrix}x \\ y \end{pmatrix}
\quad\quad\quad
\begin{pmatrix}x' \\ y' \\ z' \\ 1 \end{pmatrix}
= \begin{pmatrix}
\cos\theta & -\sin\theta & 0 & 0 \\
\sin\theta & \cos\theta & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}x \\ y \\ z \\ 1 \end{pmatrix}
$
 $
\begin{pmatrix}y' \\ z' \end{pmatrix}
= \begin{pmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta \\
\end{pmatrix}
\begin{pmatrix}y \\ z \end{pmatrix}
\quad\quad\quad
\begin{pmatrix}x' \\ y' \\ z' \\ 1 \end{pmatrix}
= \begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & \cos\theta & -\sin\theta & 0 \\
0 & \sin\theta & \cos\theta & 0 \\
0 & 0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}x \\ y \\ z \\ 1 \end{pmatrix}
$
$
\begin{pmatrix}y' \\ z' \end{pmatrix}
= \begin{pmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta \\
\end{pmatrix}
\begin{pmatrix}y \\ z \end{pmatrix}
\quad\quad\quad
\begin{pmatrix}x' \\ y' \\ z' \\ 1 \end{pmatrix}
= \begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & \cos\theta & -\sin\theta & 0 \\
0 & \sin\theta & \cos\theta & 0 \\
0 & 0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}x \\ y \\ z \\ 1 \end{pmatrix}
$
 $
\begin{pmatrix}z' \\ x' \end{pmatrix}
= \begin{pmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta \\
\end{pmatrix}
\begin{pmatrix}z \\ x \end{pmatrix}
\quad\quad\quad
\begin{pmatrix}x' \\ y' \\ z' \\ 1 \end{pmatrix}
= \begin{pmatrix}
\cos\theta & 0 & \sin\theta & 0 \\
0 & 1 & 0 & 0 \\
-\sin\theta & 0 & \cos\theta & 0 \\
0 & 0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}x \\ y \\ z \\ 1 \end{pmatrix}
$
$
\begin{pmatrix}z' \\ x' \end{pmatrix}
= \begin{pmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta \\
\end{pmatrix}
\begin{pmatrix}z \\ x \end{pmatrix}
\quad\quad\quad
\begin{pmatrix}x' \\ y' \\ z' \\ 1 \end{pmatrix}
= \begin{pmatrix}
\cos\theta & 0 & \sin\theta & 0 \\
0 & 1 & 0 & 0 \\
-\sin\theta & 0 & \cos\theta & 0 \\
0 & 0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}x \\ y \\ z \\ 1 \end{pmatrix}
$
2次元座標変換
2次元座標変換の行列
座標を
$\begin{pmatrix}
x \\
y
\end{pmatrix}$
で表すと、さまざまな幾何学変換をベクトルと行列の積で
表現できないので、同次座標 (homogeneous coordinates) を使って
座標を
$\begin{pmatrix}
x \\
y \\
1
\end{pmatrix}$
と表すことにする。
- 回転

|
$
\begin{pmatrix}x' \\ y' \\ 1 \end{pmatrix}
= \begin{pmatrix}
\cos \theta & -\sin \theta & 0 \\
\sin \theta & \cos \theta & 0 \\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}x \\ y \\ 1\end{pmatrix}
=
R(\theta)\begin{pmatrix}x\\y\\1\end{pmatrix}
$ 式(2.7)
|
- 拡大・縮小

|
$
\begin{pmatrix}x' \\ y' \\ 1 \end{pmatrix}
= \begin{pmatrix}
s_x & 0 & 0 \\
0 & s_y & 0 \\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}x \\ y \\ 1\end{pmatrix}
= S(s_x,s_y)\begin{pmatrix}x\\y\\1\end{pmatrix}
$ 式(2.6)
|
- 並行移動

|
$
\begin{pmatrix}x' \\ y' \\ 1 \end{pmatrix}
= \begin{pmatrix}
1 & 0 & t_x \\
0 & 1 & t_y \\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}x \\ y \\ 1\end{pmatrix}
= T(t_x,t_y)\begin{pmatrix}x \\ y \\ 1\end{pmatrix}
$ 式(2.5)
|
- 鏡写 (reflection)
- スキュー (skew) or せん断(shearing)



2次元座標系における合成変換
いくつかの変換を順に施す場合を、合成変換 (composite transformation) とよぶ。
たとえば、回転の中心が原点ではない場合には、
回転中心が原点と重なるように並行移動してから回転し、
その後で回転中心を元の場所に戻せばよい。

|
$
\begin{pmatrix}x'\\y'\\1\end{pmatrix}
= T(x_0,y_0) R(\theta) T(-x_0,-y_0)
\begin{pmatrix}x\\y\\1\end{pmatrix}
$ 式(2.9)
|
合成変換では変換の順序を入れ替えると、一般には同じ変換にならないことに注意が必要である。

3次元変換
3次元座標系
3次元直行座標系 (three-dimension orthogonal coordinate system) は
x軸, y軸に対してz軸がどちらを向いているかによって、
右手系 (right-handed coordinate system) と
左手系 (left-handed coordinate system) に分かれる。


簡単なモデリング
3次元図形の形状を数値的に記述することを「モデリング (modeling)」とよび、
記述される形状のデータを「形状モデル (geometric model)」とよぶ。
ここでは、ポリゴン (多角形, polygon) の集合を用いて図形を表現する方法を
紹介する。


ポリゴンにおいて、頂点数が4個以上の場合はそれらが同一平面上にあるとは限らないので、
3角形を用いることが多い。
同次座標と3次元の基本変換
2次元座標変換の場合と同様に、さまざまな変換をベクトルと行列の積として表現したいので、
3次元座標 (x, y, z) を同次座標を用いて (x, y, z, 1)として表現する。
- 回転

|
- x軸回りの回転
$
\begin{pmatrix}x'\\y'\\z'\\1\end{pmatrix}
= \begin{pmatrix}
1 & 0 & 0 & 0\\
0 & \cos \theta & -\sin \theta & 0\\
0 & \sin \theta & \cos \theta & 0\\
0 & 0 & 0 & 1\\
\end{pmatrix}
\begin{pmatrix}x\\y\\z\\ 1\end{pmatrix}
=
R_x(\theta)\begin{pmatrix}x\\y\\z\\1\end{pmatrix}
$ 式(2.19)
- y軸回りの回転
$
\begin{pmatrix}x'\\y'\\z'\\1\end{pmatrix}
= \begin{pmatrix}
\cos \theta & 0 & \sin \theta & 0\\
0 & 1 & 0 & 0\\
-\sin \theta & 0 & \cos \theta & 0\\
0 & 0 & 0 & 1\\
\end{pmatrix}
\begin{pmatrix}x\\y\\z\\ 1\end{pmatrix}
=
R_y(\theta)\begin{pmatrix}x\\y\\z\\1\end{pmatrix}
$ 式(2.20)
- z軸回りの回転
$
\begin{pmatrix}x'\\y'\\z'\\1\end{pmatrix}
= \begin{pmatrix}
\cos \theta & -\sin \theta & 0 & 0\\
\sin \theta & \cos \theta & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1\\
\end{pmatrix}
\begin{pmatrix}x\\y\\z\\ 1\end{pmatrix}
=
R_z(\theta)\begin{pmatrix}x\\y\\z\\1\end{pmatrix}
$ 式(2.21)
|
- 拡大・縮小

|
$
\begin{pmatrix}x'\\y'\\z'\\1\end{pmatrix}
= \begin{pmatrix}
s_x & 0 & 0 & 0\\
0 & s_y & 0 & 0\\
0 & 0 & s_z & 0\\
0 & 0 & 0 & 1\\
\end{pmatrix}
\begin{pmatrix}x\\y\\z\\ 1\end{pmatrix}
=
S(s_x,s_y,s_z)\begin{pmatrix}x\\y\\z\\1\end{pmatrix}
$ 式(2.18)
|
|
- 並行移動

>
|
$
\begin{pmatrix}x'\\y'\\z'\\1\end{pmatrix}
= \begin{pmatrix}
1 & 0 & 0 & t_x\\
0 & 1 & 0 & t_y\\
0 & 0 & 1 & t_z\\
0 & 0 & 0 & 1\\
\end{pmatrix}
\begin{pmatrix}x\\y\\z\\ 1\end{pmatrix}
=
T(t_x,t_y,t_z)\begin{pmatrix}x\\y\\z\\1\end{pmatrix}
$ 式(2.17)
|
|
- 鏡映

|
$
\begin{pmatrix}x'\\y'\\z'\\1\end{pmatrix}
= \begin{pmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & -1 & 0\\
0 & 0 & 0 & 1\\
\end{pmatrix}
\begin{pmatrix}x\\y\\z\\ 1\end{pmatrix}
$ 式(2.22)
|
|
- スキュー

|
$
\begin{pmatrix}x'\\y'\\z'\\1\end{pmatrix}
= \begin{pmatrix}
1 & a_{12} & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1\\
\end{pmatrix}
\begin{pmatrix}x\\y\\z\\ 1\end{pmatrix}
$ 式(2.23)
|
|
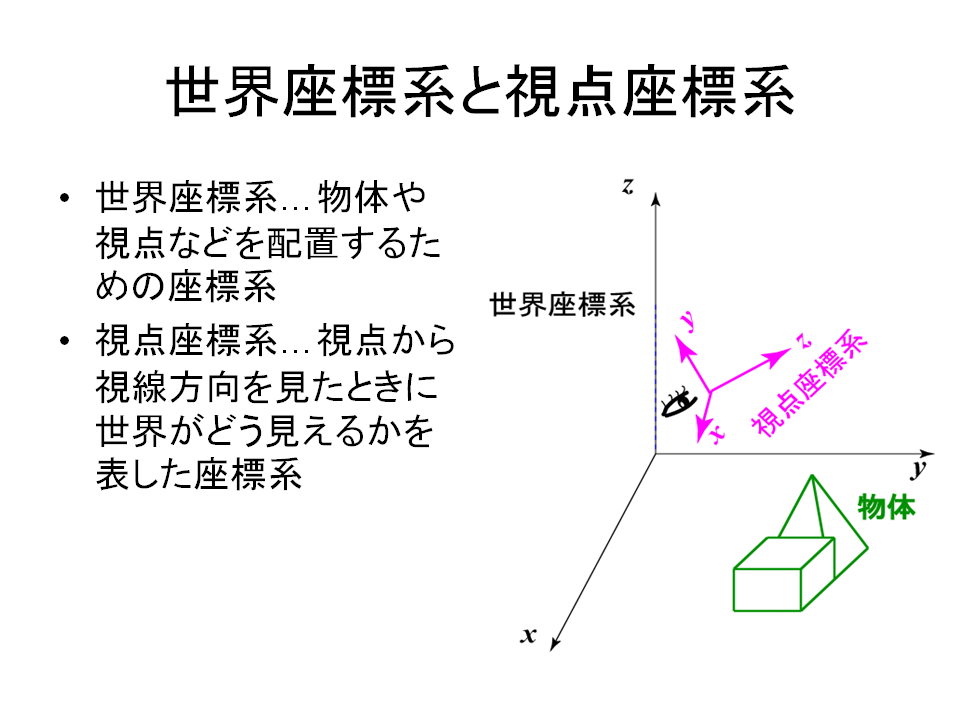
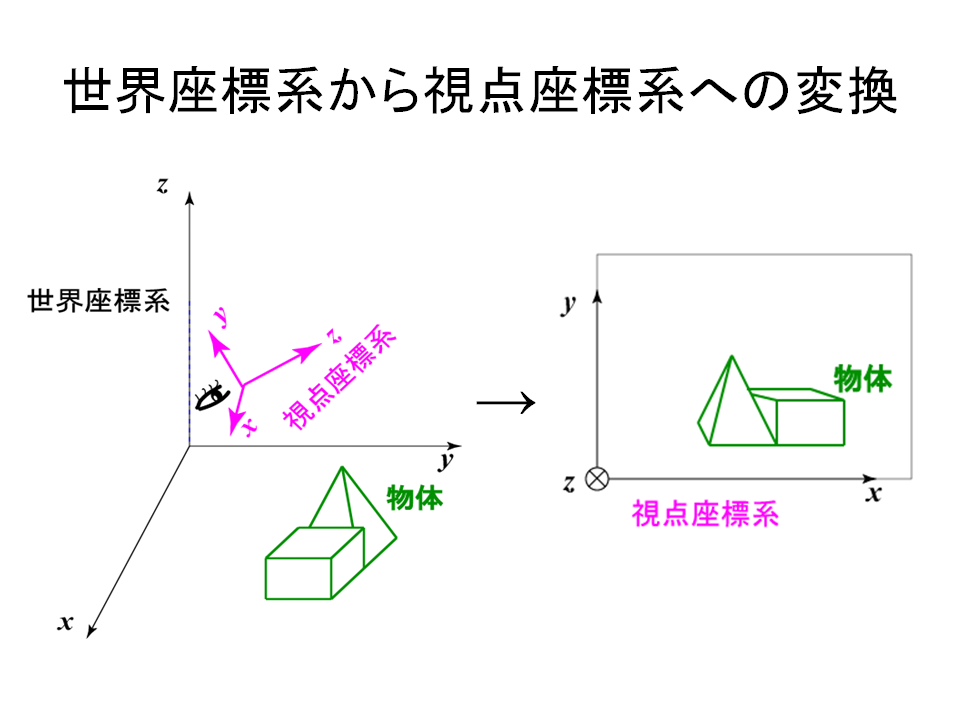
[参考] ワールド(世界)座標系からカメラ(視野)座標系への変換

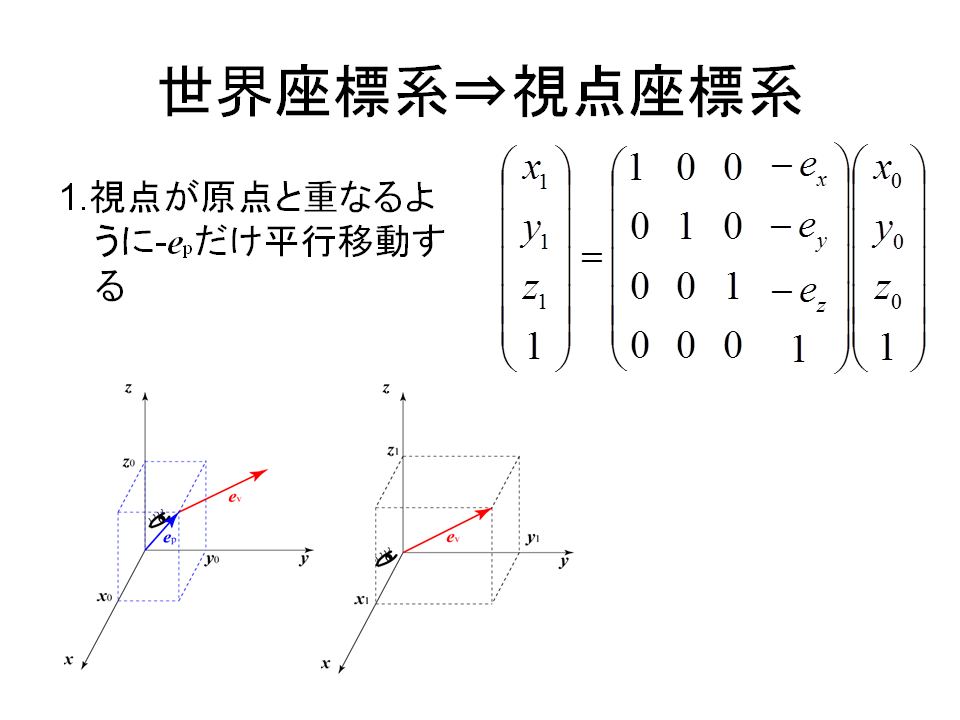
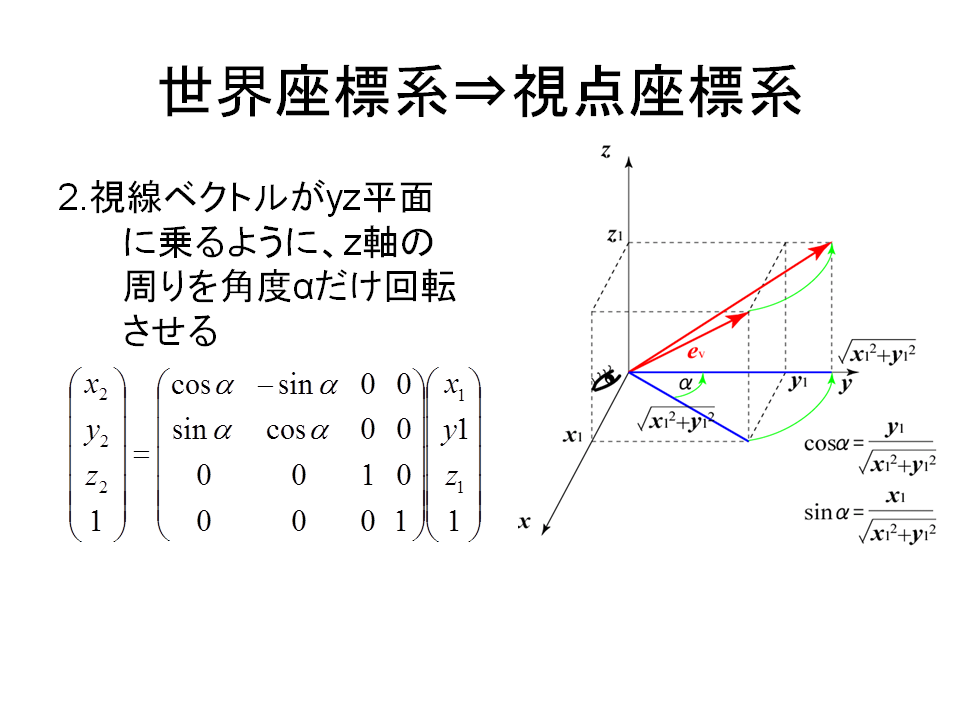
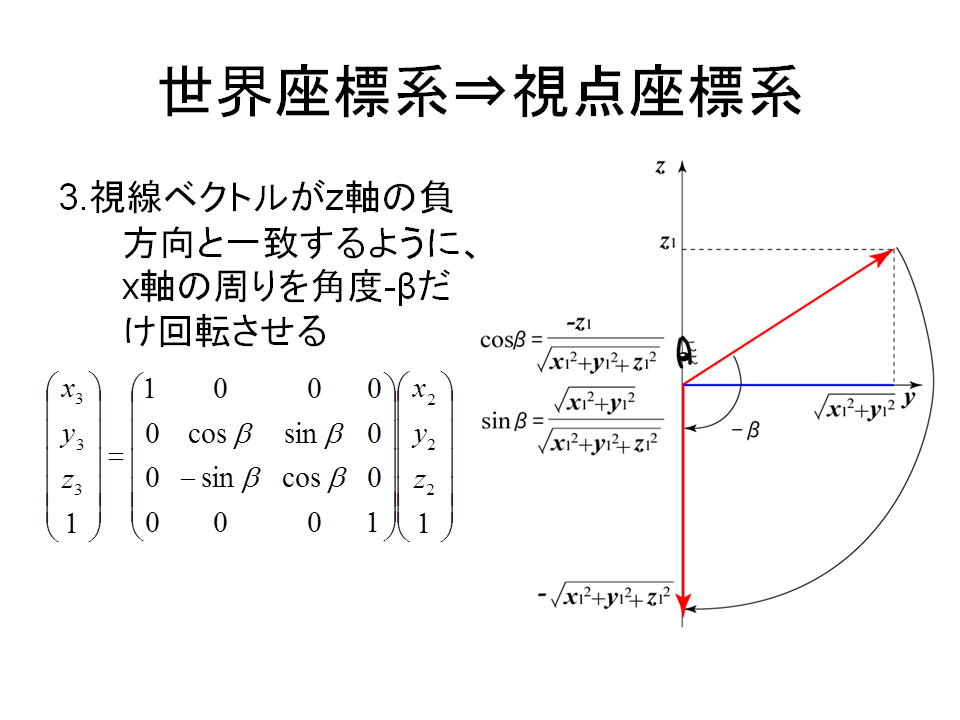
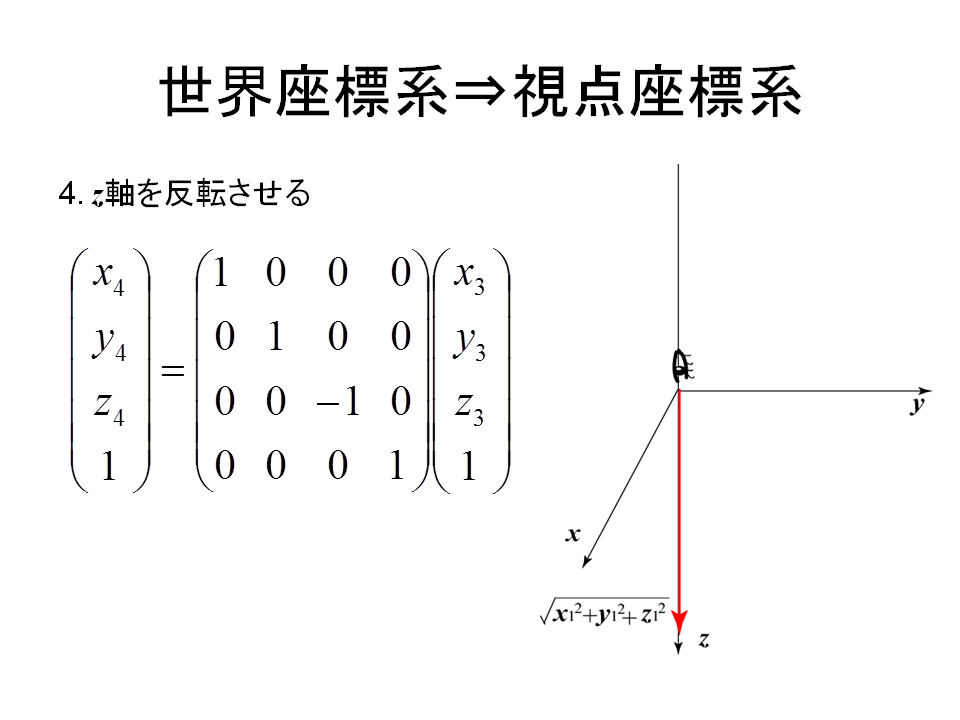











 $
\begin{pmatrix}x' \\ y' \end{pmatrix}
= \begin{pmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta \\
\end{pmatrix}
\begin{pmatrix}x \\ y \end{pmatrix}
\quad\quad\quad
\begin{pmatrix}x' \\ y' \\ z' \\ 1 \end{pmatrix}
= \begin{pmatrix}
\cos\theta & -\sin\theta & 0 & 0 \\
\sin\theta & \cos\theta & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}x \\ y \\ z \\ 1 \end{pmatrix}
$
$
\begin{pmatrix}x' \\ y' \end{pmatrix}
= \begin{pmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta \\
\end{pmatrix}
\begin{pmatrix}x \\ y \end{pmatrix}
\quad\quad\quad
\begin{pmatrix}x' \\ y' \\ z' \\ 1 \end{pmatrix}
= \begin{pmatrix}
\cos\theta & -\sin\theta & 0 & 0 \\
\sin\theta & \cos\theta & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}x \\ y \\ z \\ 1 \end{pmatrix}
$
 $
\begin{pmatrix}y' \\ z' \end{pmatrix}
= \begin{pmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta \\
\end{pmatrix}
\begin{pmatrix}y \\ z \end{pmatrix}
\quad\quad\quad
\begin{pmatrix}x' \\ y' \\ z' \\ 1 \end{pmatrix}
= \begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & \cos\theta & -\sin\theta & 0 \\
0 & \sin\theta & \cos\theta & 0 \\
0 & 0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}x \\ y \\ z \\ 1 \end{pmatrix}
$
$
\begin{pmatrix}y' \\ z' \end{pmatrix}
= \begin{pmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta \\
\end{pmatrix}
\begin{pmatrix}y \\ z \end{pmatrix}
\quad\quad\quad
\begin{pmatrix}x' \\ y' \\ z' \\ 1 \end{pmatrix}
= \begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & \cos\theta & -\sin\theta & 0 \\
0 & \sin\theta & \cos\theta & 0 \\
0 & 0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}x \\ y \\ z \\ 1 \end{pmatrix}
$
 $
\begin{pmatrix}z' \\ x' \end{pmatrix}
= \begin{pmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta \\
\end{pmatrix}
\begin{pmatrix}z \\ x \end{pmatrix}
\quad\quad\quad
\begin{pmatrix}x' \\ y' \\ z' \\ 1 \end{pmatrix}
= \begin{pmatrix}
\cos\theta & 0 & \sin\theta & 0 \\
0 & 1 & 0 & 0 \\
-\sin\theta & 0 & \cos\theta & 0 \\
0 & 0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}x \\ y \\ z \\ 1 \end{pmatrix}
$
$
\begin{pmatrix}z' \\ x' \end{pmatrix}
= \begin{pmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta \\
\end{pmatrix}
\begin{pmatrix}z \\ x \end{pmatrix}
\quad\quad\quad
\begin{pmatrix}x' \\ y' \\ z' \\ 1 \end{pmatrix}
= \begin{pmatrix}
\cos\theta & 0 & \sin\theta & 0 \\
0 & 1 & 0 & 0 \\
-\sin\theta & 0 & \cos\theta & 0 \\
0 & 0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}x \\ y \\ z \\ 1 \end{pmatrix}
$


















