コンピュータ・アーキテクチャ 第7回

順序回路

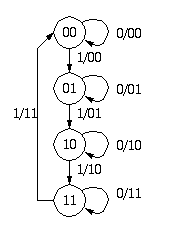
組合せ回路と記憶回路から構成され、その出力がそのときの 入力だけでなく、過去の入力の結果によって決まるような 回路を順序回路 (sequential circuit, シーケンス回路、逐次回路)といいます。

フリップフロップやその応用であるカウンタ、レジスタ、 そして複雑な電子計算機も順序回路です。

sequential circuit (順序回路; シーケンス回路; 逐次回路)
ある瞬間における出力値が,その時点での入力値と内部状態とによって定まり,その内部状態は,直前の入力値と直前の内部状態とによって定まる論理回路.
〈備考〉順序回路は,有限個の内部状態をとることができるので,抽象的な観点からは有限オートマトンとみなすことができる.

順序回路のモデル

順序回路は組合せ回路と記憶回路より構成されています。 組合せ回路の入力には、外部および記憶回路の出力が接続されます。 組合せ回路の出力は、外部および記憶回路の入力へ接続されます。

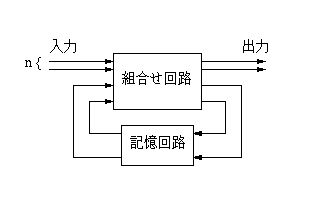
記憶回路に用いられるフリップフロップの数がm個であれば、順序回路が とり得る状態の数は 2m 通りです。 入力に n ビットが与えられれば、入力のとり得る組合せは 2n 通りです。

順序回路の状態変化を表すのが状態遷移図 (state transition diagram) です。


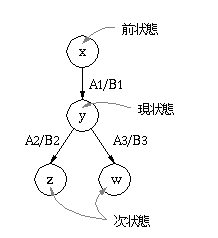
前状態 x で 入力 A1 が与えられたときに、出力B1を生じて現状態 y に なったとします。ここで、 入力 A2 が与えられると出力 B2 を生じて次状態 z になり、 入力 A3 が与えられると出力 B3 を生じて次状態 w になります。 

[2ビットカウンタ状態遷移図]

順序回路の解析

与えられた順序回路がどのように動作するかを調べて明らかにすることを 順序回路の解析 (analysis) とよびます。

以下のような順序回路を考えましょう。


$J_a = (\overline{X} + Q_a) \cdot \overline{Q_b} = \overline{X} \cdot \overline{Q_b} + Q_a \cdot \overline{Q_b} $
$K_a = Q_b $
$J_b = X $
$K_b = Q_b $
$Z = X \cdot Q_a \cdot Q_b $

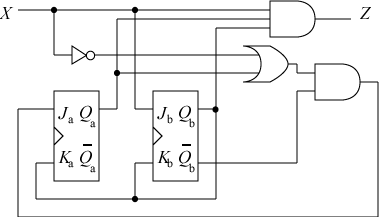
この回路の動作を調べるには、現状態と次状態を表にします。

現状態 入力 出力 次状態
$Q_a$ $Q_b$ $X$ $J_a$ $K_a$ $J_b$ $K_b$ $Z$ $Q_a$ $Q_b$
0001000010
0010010001
0100101000
0110111000
1001000010
1011010011
1100101000
1110111100

「現状態」から「次状態」への遷移を図で表すと以下のように なることがわかります。

順序回路の合成

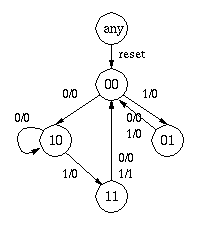
与えられた機能を持つ順序回路を実現することを、順序回路の 合成 (synthesis) といいます。 ただし、与えられた機能を実現する回路は必ずしも一義的に 決まるものではなく、種々の工夫や直観が必要な場合もあります。

[合成の手順]
  1. (文章で与えられた)問題から、回路がどのように動作すれば 所定の機能を満たすかを考え出します。
  2. 入力、出力として使用すべき信号を明らかにし、状態遷移図を作ります。
  3. 2で作った状態遷移図は原始状態図 (primitive state diagram) です。 そのなかに等価な状態が見つかれば、これを整理統合して冗長性を減らし、 最終状態図 (final state diagram) にします。
  4. 最終状態図の状態を n 個とすれば、これは $\log_2 n$ 個の フリップフロップの状態に対応させることができます。 各状態に対して各フリップフロップの 1, 0 を割り当てます。
  5. 状態割り当て (state assignment) ができれば、それから 状態遷移表を作ります。
  6. 適切な入力を作り出すための組合せ回路 (次状態デコーダ, next state decoder とよばれます) と 適切な出力を発生する組合せ回路 (出力用デコーダ, output decoder と呼ばれます)を作ります。

[例題]
入力系列を3ビット毎に区切り、その中に偶数(0も偶数に含める)個の 1を含む時、出力1を生じるような順序回路を構成しなさい。

[解答]

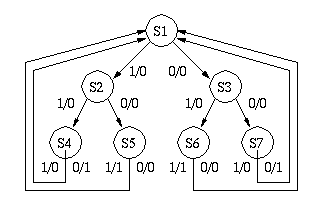
入力パターンが 000, 110, 101, 011 のときに、出力に 1 を生じるようにすればよい。 はじめに「状態1 (以降これを S1 と書くことにする)」にあるとして、 次に "1" がくるか "0" がくるかで、次の状態が異なるとして、回路の状態遷移図を作る。 たとえば、入力が 110 であると、状態はS1 -> S2 -> S4 -> S1 と変化して S4 -> S1 へ戻るときに出力 1 を生じる。 入力が 010 であると、状態は S1 -> S3 -> S6 -> S1 と変化して、出力は 0 である。

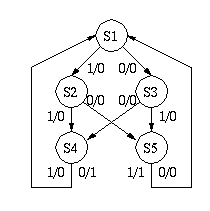
原始状態図をよく検討すると、S4 と S7 はいずれも入力 "0" で出力 "1" を生じ、 入力 "1" で出力 "0" を生じて S1 に戻る。 したがって、S4 と S7 はそれ以後の回路の動作にとって区別する必要がない状態である。 同様に S5 と S6 も区別する必要がない。 つまり、S6 と S7 は冗長な状態であり、これを省略すれば冗長な状態が存在しない、 最終状態図となる。

原始状態図最終状態図

最終状態図を見ると状態の数は5なので3bitで表現できます (22 < 5 <= 23)。 3bit で表現される 8 種類のビットパターンを5種類の状態に割り当てる 場合の数は 8!/3! = 6720 通りあります。 この割り当て方は回路の複雑さに大きく影響しますが、 一般的に使える方法は確立されていません。 

ここでは仮に以下のように割り当てたものとします。
         A  B  C
    S1:  0  0  0
    S2:  0  1  1
    S3:  0  0  1
    S4:  1  0  1
    S5:  1  1  1

状態遷移表は以下のようになります。

現状態 入力 次状態 出力
A B C X A B C Z
00000010
00010110
00101010
00111110
0100$\phi$$\phi$$\phi$$\phi$
0101$\phi$$\phi$$\phi$$\phi$
01101110
01111010
1000$\phi$$\phi$$\phi$$\phi$
1001$\phi$$\phi$$\phi$$\phi$
10100001
10110000
1100$\phi$$\phi$$\phi$$\phi$
1101$\phi$$\phi$$\phi$$\phi$
11100000
11110001

組合せ回路の入力は A, B, C, X なので、 状態遷移表から、フリップフロップの次状態を決定する 組合せ回路を作ります。 ここではDフリップフロップを使う場合を考えましょう。 存在しない 010, 110, 100 についての各項は φ (don't care) として扱います。

A, B, C それぞれのフリップフロップを FFa, FFb, FFc と表すと、 次状態デコーダのカルノーマップはそれぞれ以下のようになります。

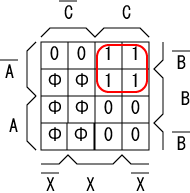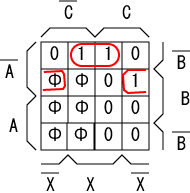FFaFFb
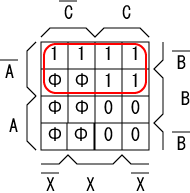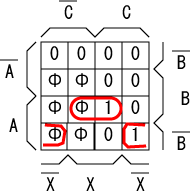FFc Z
したがって、答えは以下のようになります。

FFa の入力のための回路は $\overline{A} \cdot C$
FFb の入力のための回路は $\overline{A} \cdot (\overline{B} \cdot X + B \cdot \overline{X})$
FFc の入力のための回路は $\overline{A}$
Z (出力)のための回路は $A \cdot (B \cdot X + \overline{B} \cdot \overline{X}) $

状態割り当て

順序回路の合成では、状態の割り当て方法によって、 できあがる回路が簡単になったり複雑になったりします。 順序回路の簡単化のためには、状態割当てにも工夫が必要です。

一般に次状態デコーダが複雑になることが多いので、これを 簡単化できるような状態割当てを行ないます。

シフトレジスタとカウンタによる順序回路

不規則な回路で構成された順序回路は、設計するのが難しく、 また動作を解析するのも困難です。

見通しよく設計したり、動作を解析しやすくするためには、 シフトレジスタやカウンタなどの回路を組み合わせて 目的の回路を構成する方法をとります。

[例題]
入力系列の3ビット毎に区切り、その中に偶数(0も偶数に含める)個の 1を含む時、出力1を生じるような回路を構成せよ。

[解答]
カウンタとシフトレジスタによって構成します。
入力ビットを3ビット保持する必要があるので、Dフリップフロップ 3個 (FF3, FF4, FF5) を用います。その中に 000, 011, 101, 110 のパターンが あれば検出します。
3ビット毎に初期状態に戻すために、3進カウンタをJKフリップフロップ 2個 (FF1, FF2)で構成し、信号を FF3, FF4, FF5 のリセット信号に入れます。
FF1の出力をQ1、 FF2の出力をQ2とすると、 3進カウンタは以下のように構成できます。

現状態次状態FF2FF1
Q2Q1Q2Q1J2K2J1K1
00010φ1φ
01101φφ1
1000φ10φ
この表から作成されるFF1, FF2 のカルノーマップは以下の通りです。
     ~Q1   Q1
   +-----+-----+
~Q2|  1  |  φ |
   +-----+-----+
 Q2|  0  |  φ |
   +-----+-----+
    J1のカルノーマップ

     ~Q1   Q1
   +-----+-----+
~Q2|  φ |  1  |
   +-----+-----+
 Q2|  φ |  φ |
   +-----+-----+
    K1のカルノーマップ

J1: FF1のJ入力  (J1 = ~Q2)
k1: FF1のK入力  (K1 = 1)

     ~Q1   Q1
   +-----+-----+
~Q2|  0  |  1  |
   +-----+-----+
 Q2|  φ |  φ |
   +-----+-----+
    J2のカルノーマップ

     ~Q1   Q1
   +-----+-----+
~Q2|  φ |  φ |
   +-----+-----+
 Q2|  1  |  φ |
   +-----+-----+
    K2のカルノーマップ

J2: FF2のJ入力   (J2 = Q1)
k2: FF2のK入力   (K2 = 1)
これらから、以下のような回路構成にすればよいことがわかります。

このような構成では、問題として与えられた条件を満足することを 比較的容易に検証できます。 前の例で フリップフロップ3個で構成できた回路を、今回は フリップフロップ5個で実現しています。 これは一見無駄のように見えますが、しかし見通しがよく わかりやすい回路を設計できたという利点は大きいものです。

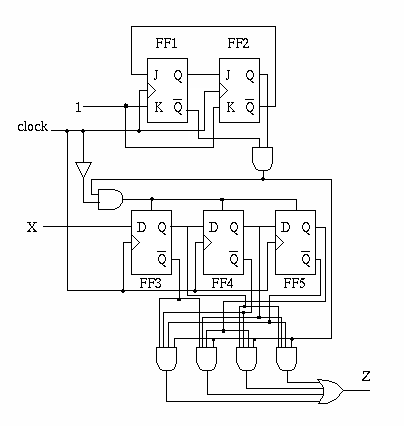
一般に、要求される回路が複雑になればなるほど、設計が単純で見通しがよく、 しかも間違いのチェックが容易な回路構成 (つまり回路としては冗長であっても、定型的で見通しがよいもの) が必要とされます。

演算回路 --- 直列加算器

シフトレジスタによる4ビット直列加算回路は以下のようになります(図 6.28参照)。 この回路ではレジスタXとYの内容を加算して、その結果を再び シフトレジスタXに入れます。 まず信号 X, Y を与え、LoadX, LoadY信号によってシフトレジスタ X, Y に 被加数、加数をそれぞれ格納します。 次に Add信号を与えてから両立シフトレジスタの内容を下位から 順番に全加算器に与えます。 全加算器の桁上がりはDフリップフロップによって、次のクロックまで 遅らせます。 加算結果は Add信号によって開かれたゲート G3 を通ってシフトレジスタ Xに戻されます。

演算回路 --- 乗算器

シフトレジスタと全加算器を用いた乗算回路の例は 図:乗算回路のようになります
図: 乗算回路
この乗算回路は3ビットと3ビットの乗算を行ないます (結果は6ビットになる可能性があります)。 結果を入れるための結果レジスタとしてFF1〜FF7の7ビットの シフトレジスタを使います。 乗数レジスタ(FF8〜FF10)はシフトレジスタですが、被乗数レジスタ (FF11〜FF13)は並列レジスタで構いません。 この回路は並列加算器として3個の全加算器が設けられていて、 被乗数レジスタの内容と結果レジスタのうちの FF4 〜 FF6 の内容を加算して 結果をレジスタの FF4 〜 FF6 に戻すようになっています。 結果レジスタには乗算の中間結果がいつでも入れられるようになっています。

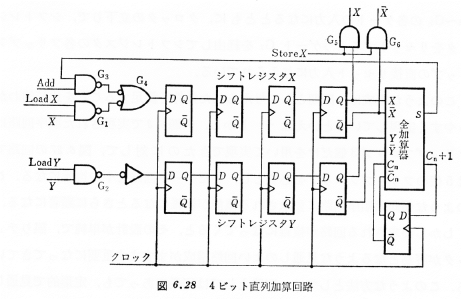
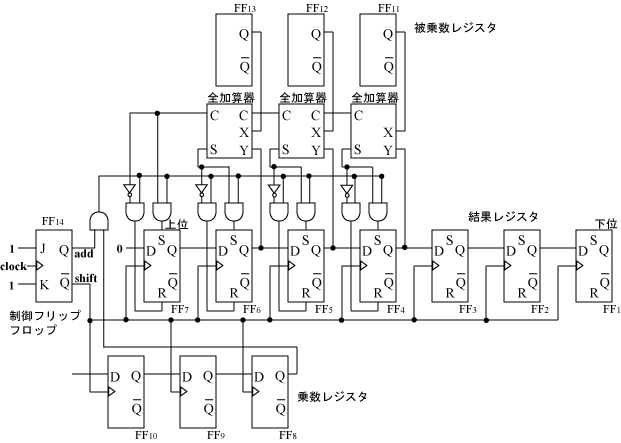制御フリップフロップ FF14 は、回路に加算動作とシフト動作を 交互に繰り返させるためのものです。 

[例題] 101 × 011 を計算するときの乗算器の動作を示して下さい。
[解答] 被乗数:  101
       乗数:    011   (1, 1, 0の順番でFF8から出力されます)
結果レジスタ:0000000
ADD101FF8の出力が1なのでADDします
結果レジスタ:0101000
Shift
結果レジスタ:0010100
ADD101FF8の出力が1なのでADDします
結果レジスタ:0111100
Shift
結果レジスタ:0011110
ADDFF8の出力が0なのでADDしません
結果レジスタ:0011110
Shift
結果レジスタ:0001111←答