コンピュータ・アーキテクチャ第6回

フリップフロップの応用

リプルカウンタ

パルスの数を数える回路をカウンタ (counter) といいます。パルスの計測には、クロックごとに出力が反転するトグル動作を利用します。カウンタ (計数器, counter) はフリップフロップの応用で最も基本的なものです。そのカウンタの中で最も簡単なのがリプルカウンタです。 4ビットリプルカウンタの構成は以下のようになります。

4個のJKフリプフロップの、JK入力は全て 1 になっています。各JKフリップフロップはクロックの立ち下がりで反転します。各フリップフロップにはリセット入力 Rd があり、ここに 1を入力するとフリップフロップはリセットされます。

リプルカウンタではフリップフロップの伝搬遅延は累加されるので後段にゆくほど影響は大きくなります。各段のフリップフロップの変化は同時には起こりませんから、たとえば $\overline{Q_0}$, $Q_1$, $\overline{Q_2}$ の AND を考えると、 4番目のクロックが立ち下がるときに一瞬だけ 1 となり、不都合が生じます。

並列カウンタ

各ビットの出力が同時に変化するのが並列カウンタ(parallel counter, 同期式カウンタ synchronous counterともいう) です。

Q0=1 のとき次の入力パルスで FF1 を反転します。 Q0=Q1=1 のとき次の入力パルスで FF2 を反転します。 Q0=Q1=Q2=1 のとき次の入力パルスで FF3 を反転します。

10進並列カウンタの構成方法

現状態				次状態
$Q_3$	$Q_2$	$Q_1$	$Q_0$	$Q_3$	$Q_2$	$Q_1$	$Q_0$
0	0	0	0	0	0	0	1
0	0	0	1	0	0	1	0
0	0	1	0	0	0	1	1
0	0	1	1	0	1	0	0
0	1	0	0	0	1	0	1
0	1	0	1	0	1	1	0
0	1	1	0	0	1	1	1
0	1	1	1	1	0	0	0
1	0	0	0	1	0	0	1
1	0	0	1	0	0	0	0

FF0のカルノーマップ	FF1のカルノーマップ
FF2のカルノーマップ	FF3のカルノーマップ

レジスタ

1つのフリップフロップは 1ビットのデータを記憶できるので、 N個のフリップフロップを用いれば Nビットのデータを記憶できます。このようにまとまったデータを記憶できる回路をレジスタ(register) といいます。

シフトレジスタ

電卓などで 3, 4, 5 という3個のデータを順番に入力すると345となります。これは順番に入力したデータを、最初のデータから上位の桁とみなしています。格納されていたデータが順番に次に移る機能をシフト機能といい、このような機能を実現した回路をシフトレジスタ (shift register) とよびます。

リングカウンタ

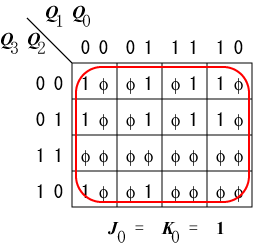
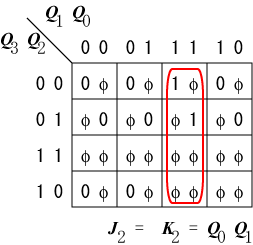
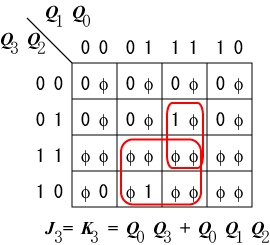
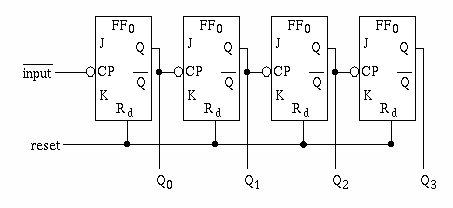
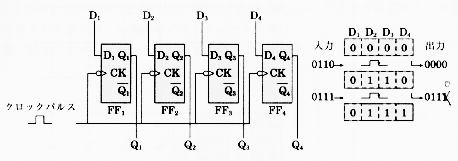
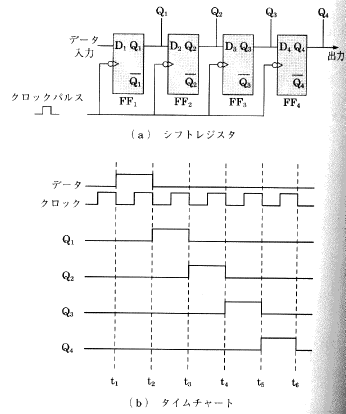
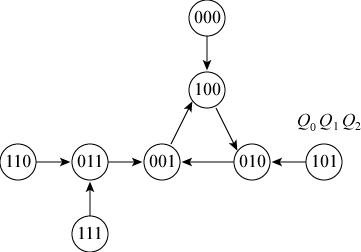
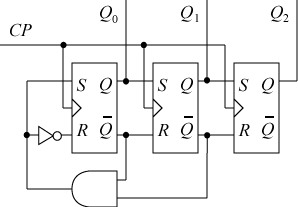
n 段のシフトレジスタのうちの1段だけに "1" を与え、他は "0" としておき、この "1" の位置をクロックパルスによってシフトすることによって計数を行なうカウンタをリングカウンタ (ring counter) といいます。

補正回路(間違った状態になっても正しい状態に移行する)を含む 3段リングカウンタは以下のようになります。

図:自己補正型3ビットリングカウンタの状態遷移

現状態			次状態
Q₀	Q₁	Q₂	Q₀	Q₁	Q₂
0	0	0	1	0	0
0	0	1	1	0	0
0	1	0	0	0	1
0	1	1	0	0	1
1	0	0	0	1	0
1	0	1	0	1	0
1	1	0	0	1	1
1	1	1	0	1	1

次状態のQ₀〜Q₂に関するカルノーマップの空白を自分で埋めてみましょう。

$Q_0$のS側

$Q_1$のS側

$Q_2$のS側

	$\overline{Q_1}$		$Q_1$
$\overline{Q_0}$	$\quad\quad$	$\quad\quad$	$\quad\quad$	$\quad\quad$
$Q_0$	$\quad\quad$	$\quad\quad$	$\quad\quad$	$\quad\quad$
	$\overline{Q_2}$	$Q_2$		$\overline{Q_2}$

	$\overline{Q_1}$		$Q_1$
$\overline{Q_0}$	$\quad\quad$	$\quad\quad$	$\quad\quad$	$\quad\quad$
$Q_0$	$\quad\quad$	$\quad\quad$	$\quad\quad$	$\quad\quad$
	$\overline{Q_2}$	$Q_2$		$\overline{Q_2}$

	$\overline{Q_1}$		$Q_1$
$\overline{Q_0}$	$\quad\quad$	$\quad\quad$	$\quad\quad$	$\quad\quad$
$Q_0$	$\quad\quad$	$\quad\quad$	$\quad\quad$	$\quad\quad$
	$\overline{Q_2}$	$Q_2$		$\overline{Q_2}$

$Q_0$のR側

$Q_1$のR側

$Q_2$のR側

	$\overline{Q_1}$		$Q_1$
$\overline{Q_0}$	$\quad\quad$	$\quad\quad$	$\quad\quad$	$\quad\quad$
$Q_0$	$\quad\quad$	$\quad\quad$	$\quad\quad$	$\quad\quad$
	$\overline{Q_2}$	$Q_2$		$\overline{Q_2}$

	$\overline{Q_1}$		$Q_1$
$\overline{Q_0}$	$\quad\quad$	$\quad\quad$	$\quad\quad$	$\quad\quad$
$Q_0$	$\quad\quad$	$\quad\quad$	$\quad\quad$	$\quad\quad$
	$\overline{Q_2}$	$Q_2$		$\overline{Q_2}$

	$\overline{Q_1}$		$Q_1$
$\overline{Q_0}$	$\quad\quad$	$\quad\quad$	$\quad\quad$	$\quad\quad$
$Q_0$	$\quad\quad$	$\quad\quad$	$\quad\quad$	$\quad\quad$
	$\overline{Q_2}$	$Q_2$		$\overline{Q_2}$

[リングカウンタの構成解答]

現状態    次状態     Q0    Q1    Q2
Q0 Q1 Q2  Q0 Q1 Q2   s r   s r   s r
 0  0  0   1  0  0   1 0   0 d   0 d
 0  0  1   1  0  0   1 0   0 d   0 1
 0  1  0   0  0  1   0 d   0 1   1 0
 0  1  1   0  0  1   0 d   0 1   d 0
 1  0  0   0  1  0   0 1   1 0   0 d
 1  0  1   0  1  0   0 1   1 0   0 1
 1  1  0   0  1  1   0 1   d 0   1 0
 1  1  1   0  1  1   0 1   d 0   d 0