組合せ回路では「与えられた機能を持つ回路を合成する」 ことが主要な問題となります。
組合せ回路の「機能」は真理値表で表現されます。 この真理値表を論理式に変換し、簡略化を行ってから、 所定のゲート回路として実現することになります。
論理回路の簡略化、最小化は昔から非常に重要な問題でした。 現在では回路の集積度も上がりコストも安くなりましたので ゲート回路を最小にする必要性は昔ほどは大きくはありません. しかし、小さなスペースで安定した回路を 実現するのはそれでもやはり重要なテーマです。
真理値表から論理式を作り、それをそのままAND, OR, NOT回路 などで構成しても正しい回路は実現できます。 しかし、そうやって作成した回路には冗長な部分が含まれますので、 論理回路として実現するには簡略化を行なう必要があります。
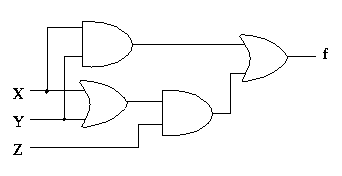
[例]多数決回路の合成
|
$\begin{eqnarray}\displaystyle f &=& \bar{X}YZ + X\bar{Y}Z + XY\bar{Z} + XYZ \quad\quad ←[*1] \\ &=& \bar{X}YZ + X\bar{Y}Z + XY\bar{Z} + XYZ + XYZ \\ &=& XY (Z + \bar{Z}) + Z(\bar{X}Y + X\bar{Y} + XY) \\ &=& XY + Z(\bar{X}Y + X\bar{Y} + XY + XY) \\ &=& XY + Z(X(Y + \bar{Y}) + Y(X + \bar{X})) \\ &=& XY + Z(X + Y) \quad\quad ←[*2]\\ \end{eqnarray}$ | ||||||||||||||||||||||||||||||||||||
| 真理値表 | 論理式の簡略化 |

|
| 回路図 |
簡略化の原理はブール代数の規則によります。 特によく使うのは以下の規則です。
$\begin{eqnarray} X + XY &=& X, \quad\quad\quad X(X+Y) &=& X ... (r1)\\ X + \bar{X}Y &=& X + Y, \quad\quad X(\bar{X} + Y) &=& XY ... (r2)\\ XY + X\bar{Y} &=& X, \quad\quad (X + Y)(X + \bar{Y}) &=& X ... (r3)\\ \end{eqnarray}$ここで (r3)は 特に重要な式で、「論理的隣接性(logical adjacency)による 簡略化」と呼ばれます。 ここで、「隣接した項」とは、 同一の変数からなる項で、一つだけの変数、たとえば$Y$が一方で$Y$ならば 他方では $\bar{Y}$ となるように異なる二つの項のことです。
[例題] 式 $f = \bar{X}\bar{Y}\bar{Z} + \bar{X}\bar{Y}Z + XY\bar{Z} + X\bar{Y}\bar{Z}$ を簡略化して下さい。
[解答]
$\displaystyle \begin{eqnarray}
f &=& \bar{X}\bar{Y}\bar{Z} + \bar{X}\bar{Y}Z + XY\bar{Z} + X\bar{Y}\bar{Z} \\
&=& \bar{X}\bar{Y}(\bar{Z} + Z) + X\bar{Z}(Y + \bar{Y}) \\
&=& \bar{X}\bar{Y} + X\bar{Z} \\
\end{eqnarray}$
[注意] 最初に $\bar{X}\bar{Y}\bar{Z}$ と $X\bar{Y}\bar{Z}$ に着目して簡略化してしまうと
$\begin{eqnarray}
f &=& \bar{X}\bar{Y}\bar{Z} + \bar{X}\bar{Y}Z + XY\bar{Z} + X\bar{Y}\bar{Z} \\
&=& \bar{Y}\bar{Z}(X + \bar{X}) + \bar{X}\bar{Y}Z + XY\bar{Z} \\
&=& \bar{Y}\bar{Z} + \bar{X}\bar{Y}Z + XY\bar{Z} \\
\end{eqnarray}$
となりこれ以上簡略化をすすめられなくなります。
見通しをもって簡略化をすすめる必要があります。
[例題] 式 $f = \bar{X}\bar{Y}\bar{Z} + \bar{X}Y\bar{Z} + XY\bar{Z} + X\bar{Y}\bar{Z}$ を簡略化して下さい。
論理的隣接性を図で表現するにはカルノーマップ (Karnaugh map) が 用いられます。 カルノーマップでは、論理的に隣接した最小項が図の上でも 隣接するように配置されています。 カルノーマップを使うと見通しよく簡略化を進めることができます。
カルノーマップは最小項を図上に配置するときに、式(r3) の意味で 隣接した最小項が図上でも隣接するような、最小項の図上配置を 行なうようなバイチ図です。
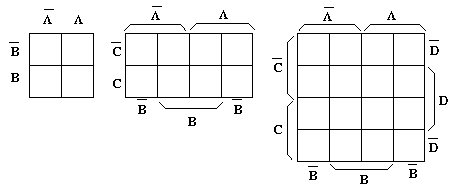
カルノーマップにしたがうと、2変数、3変数、4変数の最小項は
図のように配置されます。
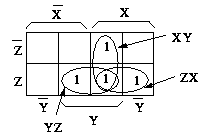
式 $f = \bar{X}YZ + X\bar{Y}Z + XY\bar{Z} + XYZ$ をカルノーマップで表すと 以下のようになり、結局 $f = XY + YZ + ZX$ と簡略化できることが わかります。
真理値はカルノーマップ上に最小項の集まりを与えます。 これから隣接性にしたがって、マップ上の全ての最小項をカバー するような集まりで、最小のものを得るようにするのが論理回路の 最小化です。 これをミニマルカバー (minimal cover) と呼びます。 カルノーマップからミニマルカバーを得る手順は次のようになります。
[例題] 以下に示すカルノーマップから簡略化された論理式を求めて下さい。
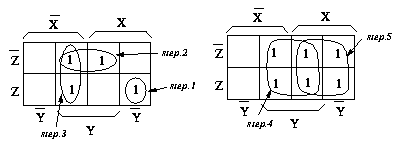
[解答]
(a) $X\bar{Y}Z$ の項は step1 で○がつく孤立項。step2で $XY\bar{Z}$ と $\bar{X}Y\bar{Z}$ の
項を囲めば、$\bar{X}YZ$ の項はstep3で取り扱われます。したがって、
$f = X\bar{Y}Z + Y\bar{Z} + \bar{X}Y$
(b) 孤立項および隣接した2項は存在せず、step4で中央の4項を囲めば、
右側の4項はstep5で囲まれます。したがって、
$f = Y + X$
[例題] 以下に示すカルノーマップから簡略化された論理式を求めて下さい。
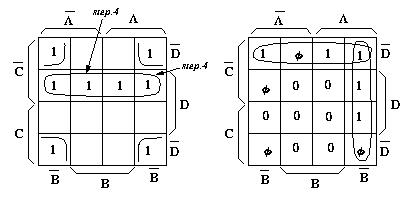
[解答]
(a) $f = \bar{C}D + \bar{B}\bar{D}$
(b) $f = A\bar{B} + \bar{C}\bar{D}$
don't care項 φ がある場合は、カルノーマップ上での簡略化の手順では 都合の良い値を "1" でも "0" でも割り当てて構いません。
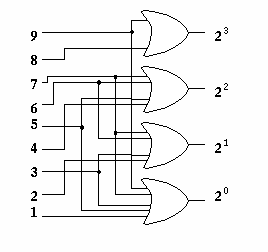
デジタル回路では2進コードで処理をするため、10進から2進への変換、 その逆の2進から10進への変換が重要となります。 そのための論理回路がエンコーダ (encoder) とデコーダ (decoder) です。
 |
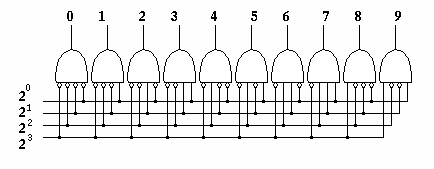 |
| エンコーダ | デコーダ |
2進法による加減剰除算の基本となるのは加算回路です。
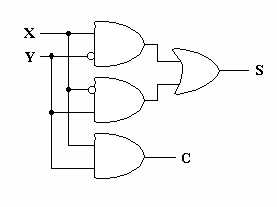
入力 X, Y を受け、その桁の和 S と、桁上がり C を作り出す、 2進1桁の回路を半加算器 (half adder) といいます。
|
$\begin{eqnarray} S &=& \bar{X} Y + X \bar{Y} \\ C &=& X Y \end{eqnarray}$ |
|
||||||||||||||||||||
| 真理値表 | 論理式 | 回路図 |
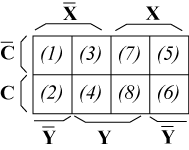
2進1桁の加算を行なうには、さらに下の桁からの桁上がりを 扱う必要があります。 このような回路を全加算器 (full adder) とよびます。
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 真理値表 | 3変数のカルノーマップ |
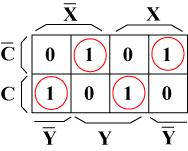 |
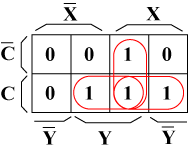 |
| Sに関するカルノーマップ | Cに関するカルノーマップ |
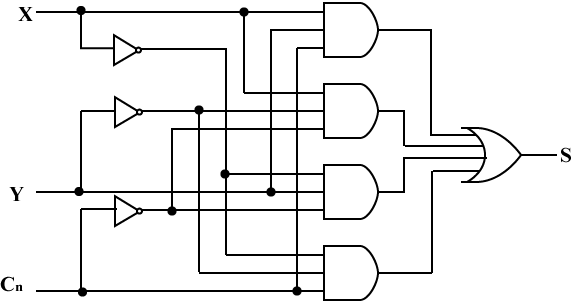
| $\begin{eqnarray} S_n &=& X_n Y_n C_n \\ &+& X_n\bar{Y}_n\bar{C}_n \\ &+& \bar{X}_nY_n\bar{C}_n \\ &+& \bar{X}_n\bar{Y}_nC_n \\ \end{eqnarray}$ | $\begin{eqnarray} C_{n+1} &=& X_nY_n \\ &+& Y_nC_n \\ &+& X_nC_n \\ \end{eqnarray}$ |
| Sに関する論理式 | Cに関する論理式 |
 |
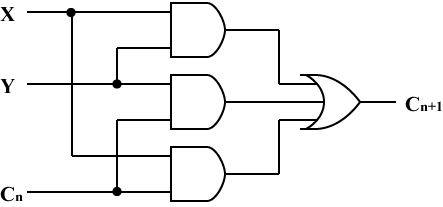 |
| Sを出力する回路 | Cを出力する回路 |
全加算器は、半加算器を2個使って以下のような回路で実現することもできます。
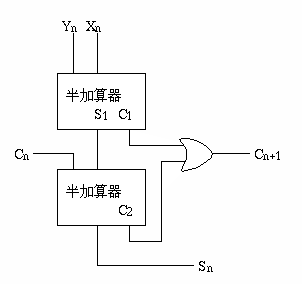 回路図
回路図
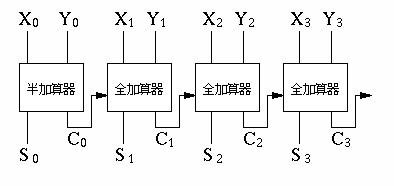
全加算器を使って、4ビットの2進数の加算を行なう回路は以下のように なります。 この回路では各桁の桁上がりは下位の桁から順に伝播してゆきます。