コンピュータ・アーキテクチャ第1回

デジタル回路と基本論理演算

情報のデジタル的表現

2進数

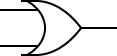
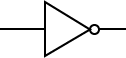
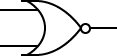
bit (ビット、binary digitの略) --- もっとも基本的な情報の単位。「ある事象が起きているか否か」を"1"または"0"の値で表現します。

[例] 1つのスイッチの開閉、1つの電球の点滅、コンデンサ内の電荷の有無

このような情報を、電子回路によって取り扱うのがデジタル回路です。

一般に、n進法では数を

$\displaystyle x = a_m n^m + a_{m-1} n^{m-1} + \cdots + a_1 n^1 + a_0 n^0 $,
$\displaystyle 0 \le a_i \le n-1 $

の形式で表現します。

2進法の場合 --- $n=2, \quad a_i=0 \; or \; 1$
10進法の場合 --- $n=10, \quad 0 \le a_i \le 9$
16進法の場合 --- $n=16, \quad 0 \le a_i \le 15$, 10以上の値はそれぞれ a, b, c, d, e, fで表現します。

[例題] 2進法で 0110 1100 となる数を、16進法および10進法で表わしなさい。
[解] 10進法で表すと 64+32+8+4=108。また4ビットずつまとめて考えて
16進数では上の桁は 4+2=6、下の桁は8+4=12 すなわち c なので 6c。
[解] 16進法で表すと 6c なので 10進法では 6 * 16 + 12 = 108 と求めても構いません。

[例題] 10進法で 158 となる数を、16進法および2進法で表わしなさい。
[解] 158 = 9 * 16 + 14 なので 16進数表現では 9e
                              2進数表現 1001 1110

[例題] 10進法で 723 となる数を、16進法および2進法で表わしなさい。
[解] $723 = 2 \times 16^2 + 13 \times 16 + 3$ なので 16進数表現では 2d3。 2進数表現 10 1101 0011

デジタル回路では電圧(電荷)が「あるか」「ないか」、すなわち 0か1の2種類の値で情報を表わします。そのため(人間にわかりやすい10進数ではなくて)2進法を用いるのが一般的です。ただし2進数で表現された数は桁が多くて人間には読みにくいため、表示するときには16進表現がよく使われています。

[注意] もちろん、2値をとるデジタル回路以外にも、多くの状態、たとえば3値を取るデジタル回路も考えることはできます。しかし、2状態だけを扱う回路の方がそれ以上の状態を扱う回路よりも実現が楽なのです。これは、たとえば、電圧の強さを 2ボルト単位で切り分けて 0 か 1 か 2 を表すシステムを考えてみれば明らかでしょう。

    0ボルト以上2ボルト未満 →"0"を表す
    2ボルト以上4ボルト未満 →"1"を表す
    4ボルト以上            →"2"を表す

このシステムでは電圧を正確に計らなくては表現している値がわかりません。「電圧がかかっていれば1、電圧がかかっていなければ0」と判断する回路の方がはるかに簡単に実現できそうなことは容易に想像がつくことでしょう。

2進演算

加算

2進における加算は、桁ごとに "1" または "0" の加算結果(S) と桁上がり(C、キャリー)を求めることによって行われます。計算は下の桁から上の桁へと行われます。

2進加算表
X	Y	S	C
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

[例] 簡単のため4bitで整数を表現して 3 + 2 を計算すると
       0011    ←10進法では3
      +0010    ←10進法では2
     ------
       0101    ←10進法では5

減算

負の数の表現

負の数を表現するためには、

符合を表わすためのビットを用いる
補数表現を用いる

という2通りの方法があります。

計算に便利なので、計算機の中では2の補数表現で負の数を表わすことが多く行なわれています。その場合は、減算は「引くほうの数を負にしてから加算する」という操作になります。

2の補数表現 --- 「各ビットを反転させて、1を足す」
加算の際に負の数を正の数と同様に扱うことができます→利点
(大きさが同じ正の数と負の数を加算すると0になります)
    nビットでは  正の数 0 〜 2^n-1-1
                 負の数 -1 〜 - 2^n-1
    が表現できます。

[例] 簡単のため4bitで整数を表現することにすると
    10進表現     16進表現     2進表現
      1            0x1         0001
     -1            0xf         1111
      2            0x2         0010
      7            0x7         0111
     -7            0x9         1001
     -8            0x8         1000

[例] 4bitで整数を表現する場合

2進数	16進数	10進数	符号付き10進数
0000	0	0	0
0001	1	1	1
0010	2	2	2
0011	3	3	3
0100	4	4	4
0101	5	5	5
0110	6	6	6
0111	7	7	7
1000	8	8	-8
1001	9	9	-7
1010	a	10	-6
1011	b	11	-5
1100	c	12	-4
1101	d	13	-3
1110	e	14	-2
1111	f	15	-1

[例] 簡単のため8bitで整数を表現することにすると
    10進表現     16進表現     2進表現
      1           0x01         0000 0001
     -1           0xff         1111 1111
     27           0x1b         0001 1011
    -27           0xe5         1110 0101
    127           0x7f         0111 1111
   -127           0x81         1000 0001
   -128           0x80         1000 0000

乗算

乗数の下一桁を調べ、それが"1"であれば被乗数を加え、"0"であればそのままにしておきます。次に、乗数の下から2桁目を調べ、被乗数を1ビット左にずらして、同様の操作を繰り返していけば2進数における乗算となります。

 [例題] 7 * 5 を2進法で計算する。
 [解]
                00000111      ← 7
                00000101      ← 5
               ----------
                00000111
               00000000
              00000111
             ------------
                00100011      ← 35

除算

2進数でも10進数の場合と同様に、

最上位の1をそろえて、被除数から除数を引く。
結果が正(または0)なら商に1を立て、負なら0を立てる。
除数を1/2して (右に1ビットだけシフトして)、上の手順を繰り返す。

という手順で計算できます。

[例題] 7/3を2進法で計算する
            ____10      ...答えは 10   つまり10進で2
       0011 ) 0111
              011
            -------
                01       ... 余りは 1

基本論理演算

論理関数

多数の入力の組合せによって、出力の値が決まるような回路を「組合せ回路」といいます。

AND, OR, NAND, NOR
X₁	X₂	AND	OR	NAND	NOR
0	0	0	0	1	1
0	1	0	1	1	0
1	0	0	1	1	0
1	1	1	1	0	0

NOT
X₁	NOT
0	1
1	0

AND, OR 回路の入力を X₁, X₂ とし、 NOT回路の入力をX₁とすると、出力は次のような論理式で表わすことができます。

 (注)$\overline{X}$ のように文字上に線を付加したい場合に、以下では ~X と表記する場合があります。

AND	OR	NOT	NAND	NOR
$X_1\cdot X_2$	$X_1 + X_2$	$\overline{X_1}$	$\overline{(X_1 \cdot X_2)}$	$\overline{(X_1 + X_2)}$

たとえば AND 回路では、入力の一方が0であれば他方の入力は出力に現れません。これを、他方の入力が出力に伝わることを一方の入力で制御していると考えて、ゲート(gate,門扉)にたとえることができます。そのため AND 回路を AND ゲートと呼ぶことがあります。さらに広げて，一般に論理回路を全てゲートと呼ぶこともあります。

ブール代数

べき等律 (idempotent law)

$X ＋ X = X$
$X \cdot X = X$

交換律 (commutative law)

$X ＋ Y = Y ＋ X$
$X \cdot Y = Y \cdot X$

結合律 (associative law)

$(X ＋ Y) ＋ Z = X ＋ (Y ＋ Z)$
$(X \cdot Y) \cdot Z = X \cdot (Y \cdot Z)$

分配律 (associative law)

$X ＋ Y \cdot Z = (X ＋ Y)(X ＋ Z)$
$X \cdot (Y ＋ Z) = X \cdot Y ＋ X \cdot Z$

また、ブール代数には 0 と 1 という要素があり次の公理を満たす。

$1 ＋ X = 1$
$0 \cdot X = 0$
$0 ＋ X = X$
$1 \cdot X = X$

相補律 (complementary law) ←否定はこの公理を満足する単項演算

$X+\overline{X}=1$
$X \cdot \overline{X} = 0$

双対律 (dualization law) ←ド・モルガンの定理(de Morgan's theorem)

$\overline{(X \cdot Y)} = \overline{X} ＋ \overline{Y}$
$\overline{(X ＋ Y)} = \overline{X} \cdot \overline{Y}$

対合律 (involution law)

$\overline{(\overline{X})} = X$

吸収律 (absorption law)

$A + (A \cdot B) = A$
$A \cdot(A + B) = A$

吸収率は真理値表を書いて確認しておきましょう。また、それから、結合律の最初の式も確認しておきましょう。

ブール代数の応用

集合論では、ブール代数の関係はフェン図 (Venn diagram) で表現します。

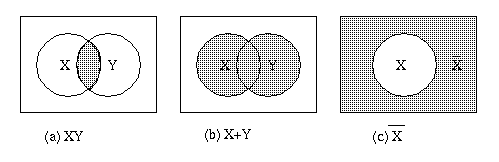
フェン図と同様の集合の表現としてバイチ図 (Veitch diagram) があります。バイチ図は論理回路の説明に便利です。

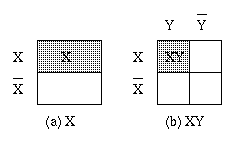
たとえば $X ＋ (X \cdot Y) ＝ X$ は上のバイチ図より明らかでしょう。

リレー接点

リレー接点を用いた論理回路では接点が閉じていることを "1" に、開いていることを "0" に対応させます。ブール代数によるリレー回路の表現の例を以下に示します。

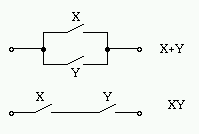
[例題] 次に示すリレー回路をブール代数式で表しなさい。

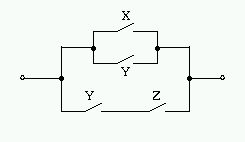
上側の回路は X+Y 、下側の回路は $Y \cdot Z$ 、この2つの回路が OR関係になっているので、回路全体は $(X+Y) + (Y \cdot Z)$ となります。

展開定理と標準形

論理関数 $G(X_{1},X_{2}, ..., X_{n})$ を考えます。
いま$X_{1}$に着目し、

$X_{1}=1$ のときの論理関数 $G_{1}(X_{2},...,X_{n}) = G(1,X_{2}, ..., X_{n})$
$X_{1}=0$ のときの論理関数 $G_{0}(X_{2},...,X_{n}) = G(0,X_{2}, ..., X_{n})$

を考えると、

$G(X_{1},X_{2},...,X_{n}) = X_{1} G_{1}(X_{2},...,X_{n}) + \overline{X_{1}} G_{0}(X_{2},...,X_{n})$
$= X_{1} G(1,X_{2},...,X_{n}) + \overline{X_{1}} G(0,X_{2},...,X_{n})$

が成立します。これは$G(X_{1},X_{2},...,X_{n})$を$X_{1}$で展開したものです。
さらに $X_{2}$ について展開すると

$G(1,X_{2},...,X_{n}) = X_{2} G(1,1,X_{3},...,X_{n}) + \overline{X_{2}} G(1,0,X_{3},...,X_{n})$
$G(0,X_{2},...,X_{n}) = X_{2} G(0,1,X_{3},...,X_{n}) + \overline{X_{2}} G(0,0,X_{3},...,X_{n})$

となりますから、結局

$G(X_{1},X_{2},...,X_{n}) = X_{1} X_{2} G(1,1,X_{3},...,X_{n}) + X_{1} \overline{X_{2}} G(1,0,X_{3},...,X_{n})$
$+ \overline{X_{1}} X_{2} G(0,1,X_{3},...,X_{n}) + \bar{X_{1}} \bar{X_{2}} G(0,0,X_{3},...,X_{n})$

となり、これを繰り返すと

$G(X_{1},X_{2},...,X_{n}) = \bar{X_{1}} \bar{X_{2}} \cdots \overline{X_{n}} G(0,0,...,0)$
$+ \bar{X_{1}} \bar{X_{2}} \cdots X_{n} G(0,0,...,1)$
$\cdots$
$+ X_{1} X_{2} ... X_{n} G(1,1,...,1)$

となります。このように任意の論理回路が展開できることを展開定理とよび、得られた式を加法標準形 (disjunctive canonical form) とよびます。

[例題2.1]

ブール関数 $G(X_{1},X_{2},X_{3}) = \bar{X_{1}} \bar{X_{2}} + X_{2} X_{3} + X_{1} \bar{X_{3}}$ を加法標準形で表せ。

[例題2.1 解答]

$G$ の $X_{1}$, $X_{2}$, $X_{3}$ にそれぞれ 0,1を代入すると

$G(0,0,0)=G(0,0,1)=G(0,1,1)=G(1,0,0)=G(1,1,0)=G(1,1,1)=1$
$G(0,1,0)=G(1,0,1)=0$

となるから

$G(X_{1},X_{2},X_{3}) = \bar{X_{1}} \bar{X_{2}} \bar{X_{3}} + \bar{X_{1}} \bar{X_{2}} X_{3} + \bar{X_{1}} X_{2} X_{3} + X_{1} \bar{X_{2}} \bar{X_{3}} + X_{1} X_{2} \bar{X_{3}} + X_{1} X_{2} X_{3}$

[注]加法標準形は、結果が 1 となる変数の組合せについて、その変数 $x$ が1のときには $x$, 0のときには $\overline{x}$ を乗じて得られた項を + 記号で連結すれば得られることがわかります。

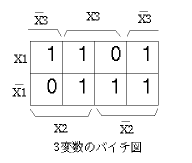
フェン図やバイチ図で n変数の論理回路を表現すれば、一般に 2ⁿ 個の領域が必要となります。その各領域は、論理関数の各変数(~がつく場合もある)の積によって表されます。この積は基本積 (fundamental product) と呼ばれ、ひとつの基本積はバイチ図上のひとつの領域を表します。この領域は変数の数を決めれば、バイチ図上で表される最小の領域でありこれを表すブール代数の基本積は最小項 (miniterm) と呼ばれます。

[例題2.2]

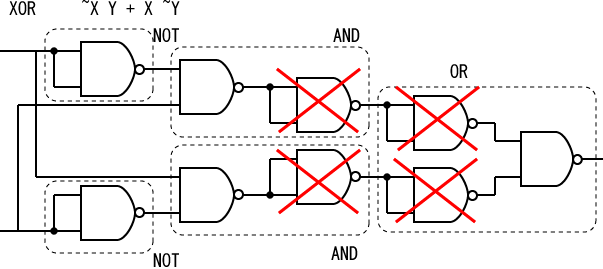
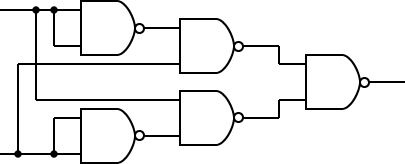
以下に示す真理値表を論理関数で表し、この論理関数を実現する回路を AND, OR, NOT回路を使用して設計してみましょう。これを XOR (Exclusive OR, 排他的論理和)と言います。

X	Y	f
0	0	0
0	1	1
1	0	1
1	1	0

[例題2.2 解答]

[例題2.3]

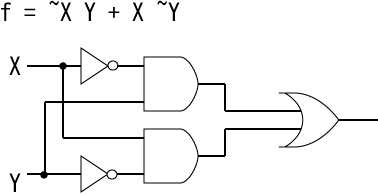
次に示す真理値表を満足する論理関数を加法標準形で求めなさい。

X	Y	Z	f (出力)
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0

[例題2.3 解答]

$f=\overline{X} Y Z + X \overline{Y} Z + X Y \overline{Z}$

[例題2.4]

NOR回路のみで次の回路を合成しなさい。
(a) NOT (b) AND (c) OR (d)XOR

[例題2.4 解答]

[例題2.5]

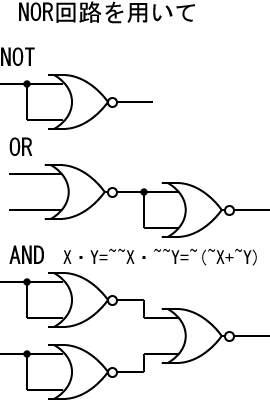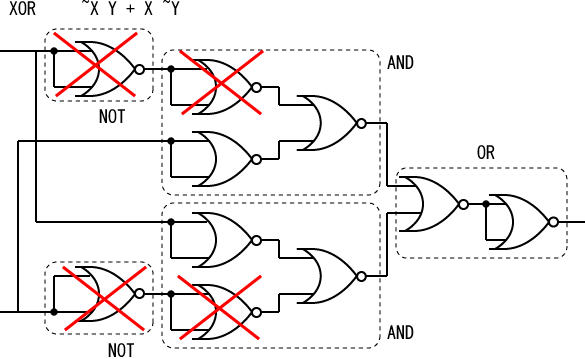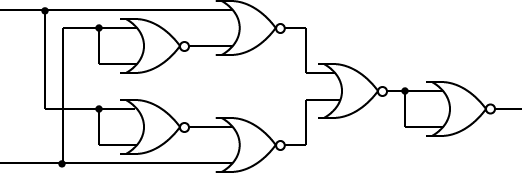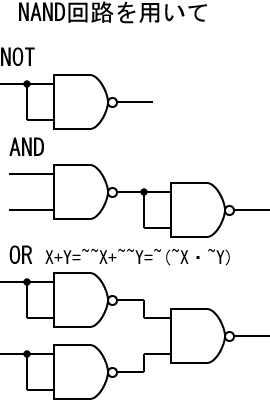
NAND回路のみで次の回路を合成しなさい。
(a) NOT (b) AND (c) OR (d)XOR

コンピュータ・アーキテクチャ 第1回