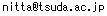アルゴリズムc 第9回
最大流
問題の定義は、
https://ja.wikipedia.org/wiki/%E6%9C%80%E5%A4%A7%E3%83%95%E3%83%AD%E3%83%BC%E5%95%8F%E9%A1%8C
によると以下の通りです。
最大フロー問題または最大流問題(英: Maximum flow problem)とは、単一の始点から単一の終点へのフローネットワークで最大となるフローを求める問題である。単にフローの最大値を求める問題と定義されることもある。最大フロー問題は、より複雑なネットワークフロー問題である最小費用流問題の特殊ケースと見ることもできる。
最小カット問題(英: Minimum cut problem)とは、辺の重みが非負値の有向グラフにおいて、始点から終点までのパスが存在しなくなるように辺を除去した時に、除去した辺の重みの総和を最小にする問題。始点から終点への最大フローは始点から終点への最小カットと等しい。これを最大フロー最小カット定理と呼ぶ。
2部グラフの最大マッチング問題(英: Maximum bipartite matching)とは、2部グラフの最大マッチングを求める問題で、これも最大フロー問題のアルゴリズムを使用して解ける。
|
 |
|
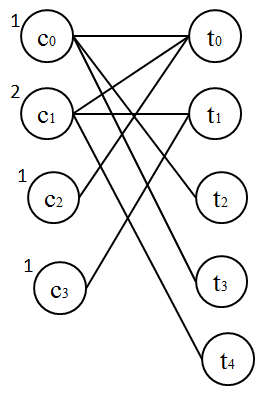
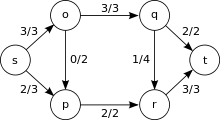
最大フローのあるフローネットワークの例。始点 s と終点 t があり、各枝の数値はフローと容量を示す。
|
Wikipedia の定義はちょっとわかりにくいですが、要は、グラフの上で流れ(フロー)を扱うということです。
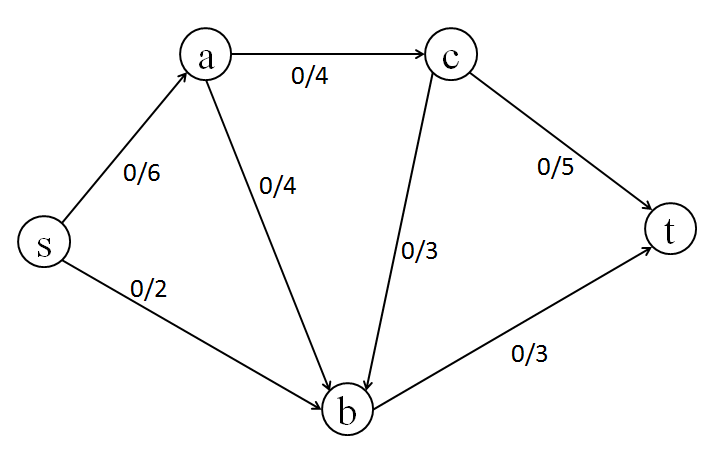
例として、次の5個のノード s, t, a, b, c から構成される有向グラフを考えます。
グラフで、ノード s からノード t に流せる最大の流量はいくらになるでしょうか?
グラフ中のエッジの「流量 (flow)」と「容量(最大流量, capacity)」を '流量/容量' の形式で表現しています。
 |
[1] ノード s では無限量の水が湧き出していて、ノード t では無限量の水を排水できるものとします。
sからt に流れる水の最大流量はどうなるでしょうか?
|
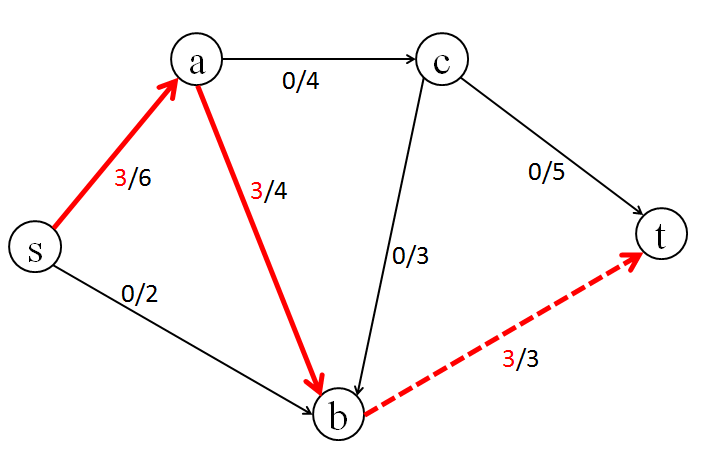 |
[2] まず、s -> a -> b -> t のパスに沿って、流量 3 で流してみます。
グラフ中で b -> t の有向エッジの流量が容量(最大流量)に達したので、点線で表しています。
|
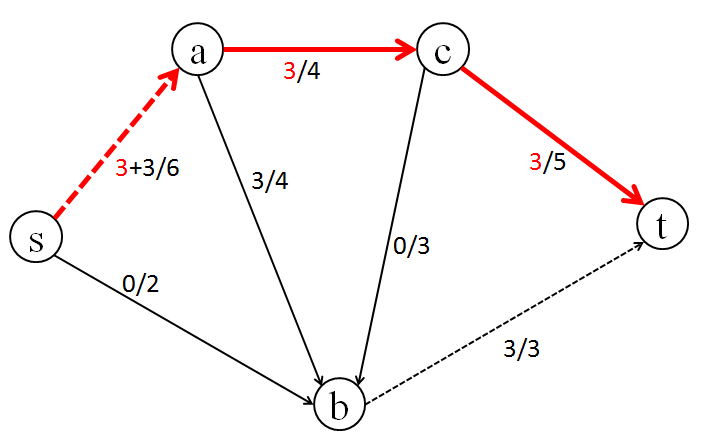 |
[3] 次に、s -> a -> c -> t のパスに沿って、流量 3 で流してみます。
グラフ中で s -> a の有向エッジの流量は容量(最大流量)に達したので、点線で表しています。
|
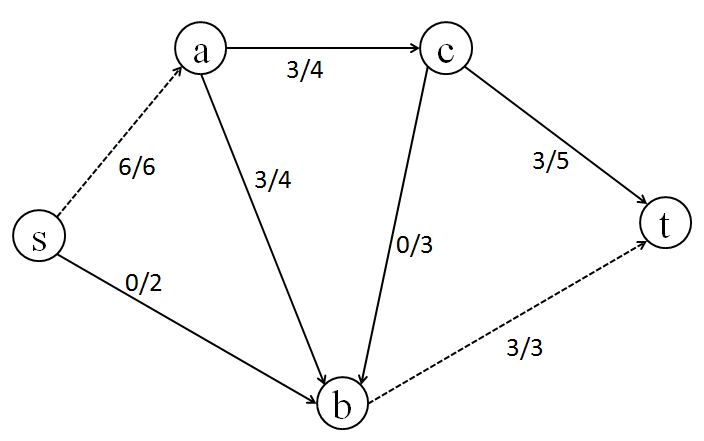 |
[4] 左のグラフをみると、もうs から t へむかうパスは存在しないように見えます。
ではsからt への最大流は 3+3=6 なのでしょうか?
|
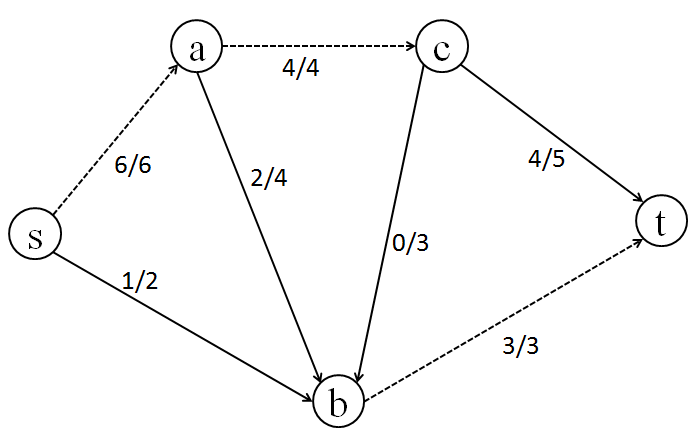 |
[5] 実は、次のように流すことで s から t へは 7 の流量を流すことができ、最大流は 7 であることがわかります。
|
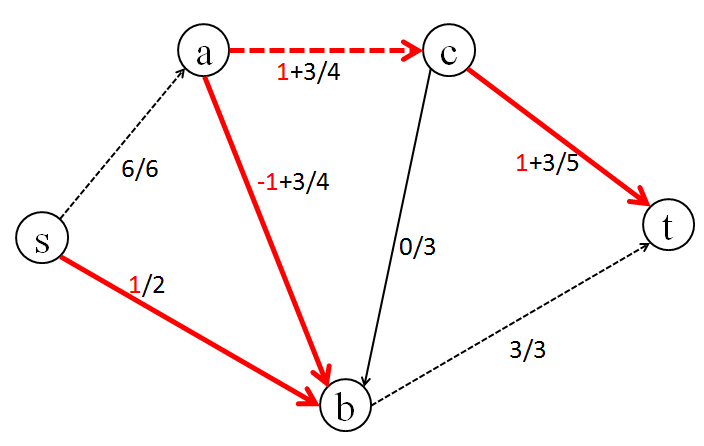 |
[6] [4]と[5]のグラフではどこが違うのでしょうか?
異なる流れを赤で示しました。
すなわち、a -> b への流量3を1だけ押し戻す ことで
s -> b -> a -> c -> t へ 1 の流量を流していることになります。
|
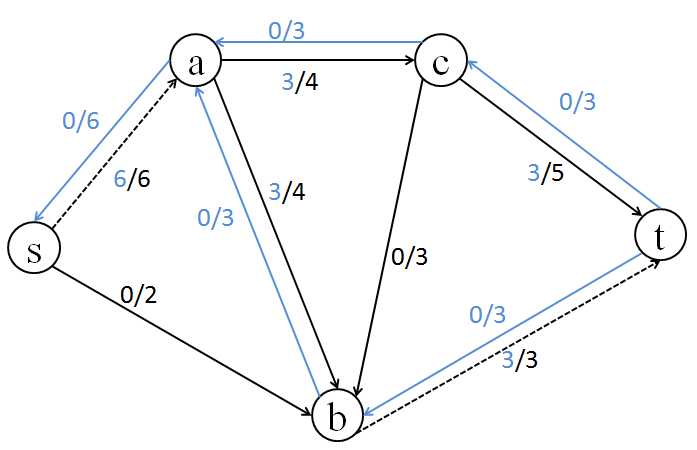 |
[7] そうです。あるエッジを流れる流量が n の状態では、逆方向に 0 〜 n の流量を流せるエッジが存在すると考えるべきなのです。
[4]のグラフに逆方向のエッジを加えたグラフを左に示します。
この逆方向のエッジを流れる水は流れを押し戻していることに相当します。
|
最大流を解くプログラム
最大流を解くプログラムの例を示します。
このプログラムでは、有向エッジを
- 終点ノード to
- 残された容量 cap
- 対になる逆向きのエッジ rev (ノードtoのrev番目のエッジ)
を持つ Edge クラスで表現しています。
各ノードが持つ情報はそのノードを起点とする有向エッジの集合 ArrayList<Edge> であり、
それをまとめた ArrayList<ArrayList<Edge>> がノードの集合で、グラフを表しています。
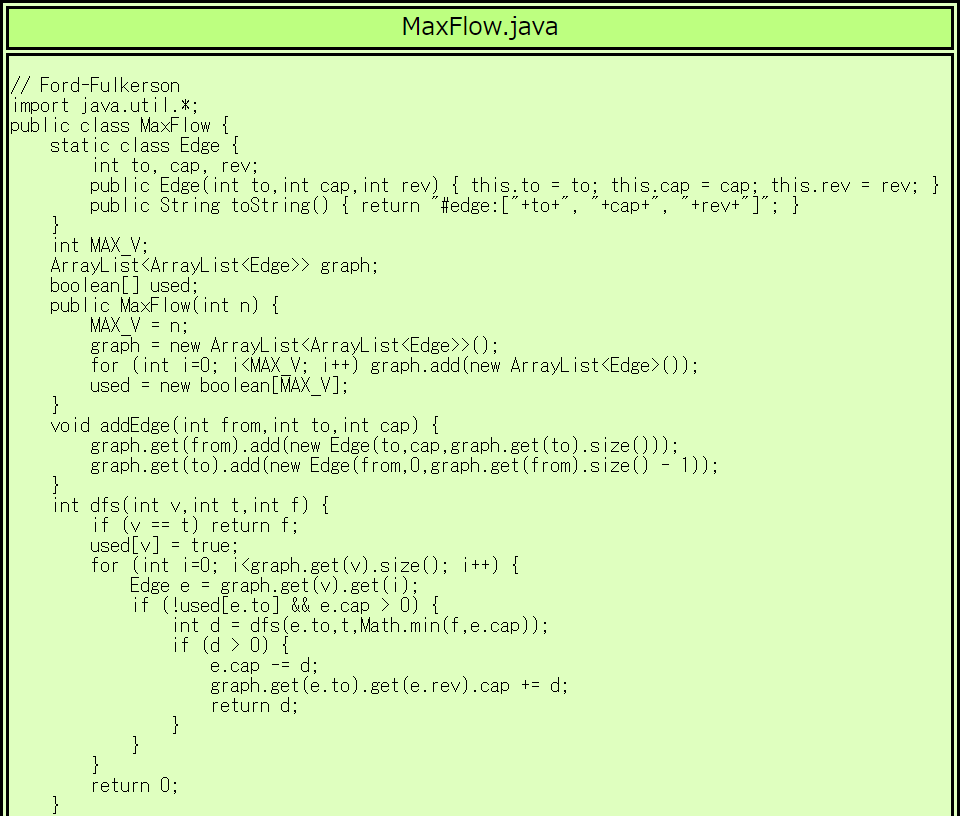
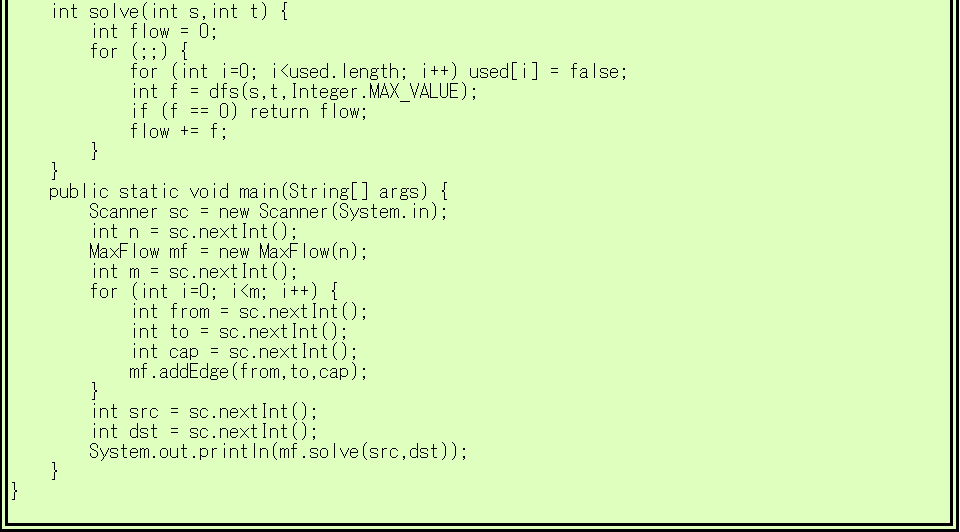
| MaxFlow.javaの実行例 |
$ javac MaxFlow.java
$ java MaxFlow < data01.txt
7
|
| data01.txt |
5 7
0 1 6
0 2 2
1 2 4
1 3 4
2 4 3
3 2 3
3 4 5
0 4
|
入力データの形式
N E
S 1 D 1 C 1
...
S E D E C E
F T
|
N はノードの数で
E はエッジの数。
S i は i番目のエッジの始点ノード番号で
D i は i番目のエッジの終点ノード番号で、
C i は i番目のエッジの容量を表す。
ただし、
0 ≤ S i < N , 0 ≤
0 ≤ D i < N 。
F と T はそれぞれ湧き出しと排水のノード番号である。
|
最小カット
|
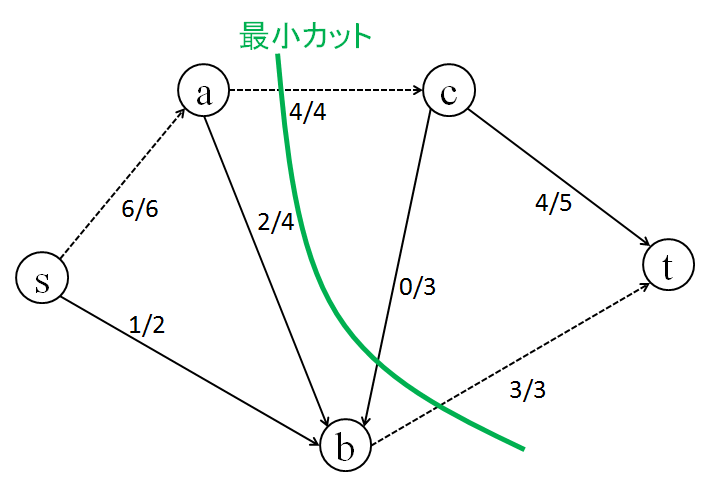
グラフ中のノードを、ノードs を含む集合 S と、ノードt を含む集合 T に分けます。
「ノードの集合から出て行くエッジ」の集合を「カット」と呼び、
「Sに含まれるノード」から「Tに含まれるノード」へと向かうカットを特に「s-t カット」と呼びます。
「s-tカット」に含まれるエッジを全て除去すると、sからtへのパスが存在しなくなります。
「sからtへのパスが存在しなくなるために除去しなければならないエッジの容量の和の最小値」を「最小カット」といいます。
「最小カット」と「最大流」は一致します。左の図ではどちらも 7 になります。
|
二部グラフのマッチング
「ノードの集合を2つの部分集合に分割したときに、部分集合内のノード同士にはエッジが無いようにできるグラフ」
を「二部グラフ (Bipartite graph)」といいます。
また、グラフにおいて「端点を共有しないエッジの集合」を「マッチング」といいます。
二部グラフにおいて最大のマッチングを求める問題は、最大流で解くことができます。(課題9a)
 |
応募者 ci は3名で、仕事 tj が3個ある。
応募者は全員1個の仕事を希望している。
希望する仕事はそれぞれ
c0はt0 か t1,
c1はt0 か t2,
c2はt0
である。
|
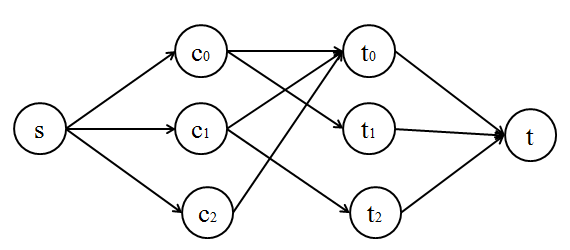 |
ノード s と t を作り、sとciを、
tiとtを、容量1 の有向エッジで結ぶ。
また、ci がtj を希望する場合は、容量1の有向エッジで結ぶ。
|
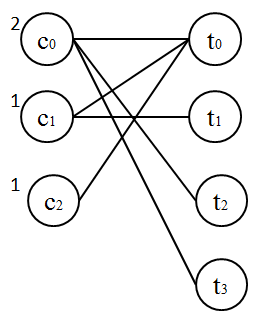 |
応募者 ci は3名で、仕事 tj は4個ある。
応募者c0は2個の、c1 と c2 は1個の仕事を希望している。
希望する仕事はそれぞれ
c0はt0 か t2 か t3,
c1はt0 か t1,
c2はt0
である。
|
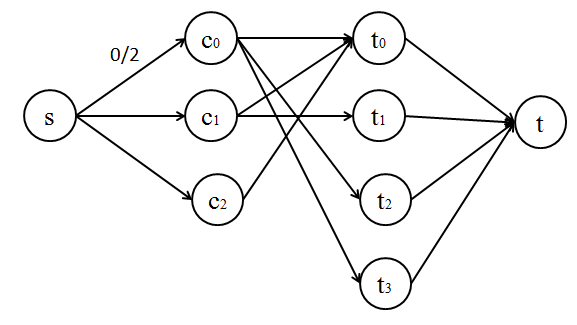 |
ノード s と t を作り、
sとc0を容量2の有向グラフで、
sとc1,
sとc2
を容量1の有向エッジで結ぶ。
tiとtを、容量1 の有向エッジで結ぶ。
また、ci がtj を希望する場合は、容量1の有向エッジで結ぶ。
|
最小費用流
各エッジに流量に応じて発生するコストがある場合を考えます。
sからtへ流量 F を流したときの最小費用を求める問題が、最小費用流です。
基本的な考え方は最大流と同じですが、sからtへのパスを探すときに毎回コストが最小となるパスを求めていけばよいのです。
これは負の重みを持つグラフの最短経路を求める話になりますから、ダイクストラ法では駄目で、Bellman-Ford法を用いて
sからtへのパスを探すことになります。
アルゴリズムc 演習
作成したプログラムが正しく動作することを確認したら、それぞれの
提出先に提出しなさい。
提出した後は、正しく提出されていることを
http://ynitta.com/class/algoC/local/handin/
で必ず確認しておいて下さい。
課題提出〆切は次回の講義の開始時刻です。
課題9a
問題を解くプログラム BipartiteMatch.java を作成せよ。
MaxFlow クラスを外部から呼び出して構わない。
問題
アルバイトに応募してきた人に、仕事を割り振るプログラムを考えます。
条件は次の通りです。
- 応募者によって可能な仕事数は異なる。
- 応募者に、希望しない仕事が割り当てられることはない。
- 一つの仕事が、複数の応募者に割り当てられることはない。
- なるべく多くの仕事を割り当てたい。
入力データの形式
N M E
C 1
...
C N
S 1 D 1
...
SE D E
|
N は応募者の数、
M は仕事の数、
E は応募者と希望した仕事との対応の数である。
C i は i番目の応募者が可能な仕事の数である。
S j と D j は S j 番目の応募者が
希望する仕事が D j であることを表している。
0 ≤
S j
< N , 0 ≤
D j
< M である。
|
| bipartite01.txt |
3 3 5
1
1
1
0 0
0 1
1 0
1 2
2 0
|
| bipartite02.txt |
3 4 6
2
1
1
0 0
0 2
0 3
1 0
1 1
2 0
|
| BipartiteMatch.javaの実行例 |
$ javac BipartiteMatch.java
$ java BipartiteMatch <bipartite01.txt
3
$ java BipartiteMatch <bipartite02.txt
4
$ java BipartiteMatch <bipartite03.txt
4
|
ヒント
ノードの数が n + m + 2 個の有向グラフで表現できる。
たとえば、ノード番号を
応募者: 0...(n-1),
仕事: n...(n+m-1)
src: (n+m)
dst: (n+m+1)
とすればよい。応募者が希望する仕事数が src とその応募者を結ぶエッジの容量で、それ以外のエッジの容量は全て1である。