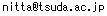アルゴリズムc 第8回
(注意)python版はこちら。
Dynamic Programming (動的計画法)
Edit Distance (編集距離)
「ある文字列 s と別の文字列 t がどれだけ似ているか」
を判断したい場合があります。
それを表すのが編集距離 (Edit Distance) という概念です
(レーベンシュタイン距離, Levenshtein distance とも言います)。
編集距離が小さいほど「近い」、すなわち「似ている」ということになります。
文字列 s に次の3種類の操作を加えて、文字列 t
に変更するのにかかる手間が編集距離です。
3種類の操作それぞれにコスト(cost, 手間)が設定されるのが普通です。
- 置き換え(substitute) ... sの中の1文字を別の1文字で置き換える。
例 apble → apple
- 挿入(insert) ... sの中に1文字を挿入する。
例 aple → apple
- 削除(delete) ... sの中の1文字を削除する。
例 applet → apple
編集距離を計算するためには、動的計画法を用います。
この方法では、長さnと長さmの文字列の間の編集距離を求めるに
(n+1)×(m+1)の2次元行列の各要素を計算で求めていくので、
計算量はO(mn)です。
編集距離の計算例
"saka"という文字列から"ara"という文字を生成するときに
コストが最小となるような編集操作を考えます。
文字列"saka"のうち再利用できる部分は再利用しながら消費して、
なるべく効率良く文字列"ara"を生成したいわけです。
動的計画法で解くには、元の(消費すべき)文字列を縦に、
生成すべき文字列を横に書いた表を用います。
各文字列の先頭は一マス分空けておきます。
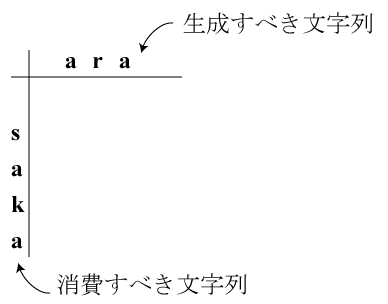
この表の中の各マスに対応する編集中の文字列の状態は次のようになります。
ここではカーソル位置を'|' (vertical bar, 縦棒)で表現しています。
カーソル位置の左にある文字(赤色で表現しています)は既に生成した文字列で、
カーソル位置の右にある文字(緑色で表現しています)は元の文字列のうち
まだ消費していない文字列です。
| | a | r | a |
| |saka | a|saka | ar|saka | ara|saka |
| s | |aka | a|aka | ar|aka | ara|aka |
| a | |ka | a|ka | ar|ka | ara|ka |
| k | |a | a|a | ar|a | ara|a |
| a | | | a| | ar| | ara| |
最小コストを求めるだけならば表は1つでいいのですが、
編集操作の手順を記録しておく必要がある場合は表をもう1つ用意します。
今回の例ではそれぞれの操作のコストを以下のように仮定します。
もちろんこれらの値はどのように設定しても構いません。
文字列を編集している位置をここでは「カーソル位置」と表現しています。
| 操作 | 記号 | コスト | 説明 |
|---|
| Insert | I | 1 | カーソル位置の直前に1文字を挿入します。 |
| Delete | D | 1 | カーソル位置の直後にある1文字を削除します |
| Substitute | S | 1 | カーソル位置の直後にある1文字を置き換え、カーソル位置を書き換えた文字の直後に移動します |
| Match | M | 0 | カーソル位置を1文字分後ろに移動します |
以下では、表の L行R列要素を(L,R)と表現しています。
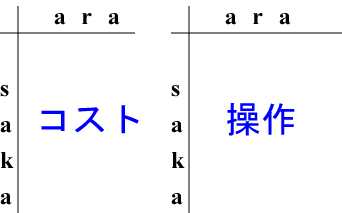 |
2つの表のうち、左の表はコストを記録します。
右の表は最小コストを決定したときに最後に行った操作を記録します。
|
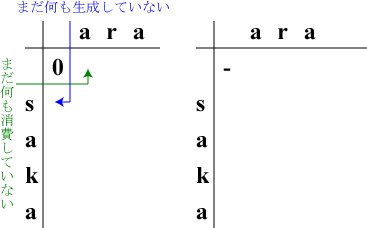 |
左表の(0,0)にコスト0と記入しましょう。
右表の(0,0)はまだ何も操作を行っていないので"-"です。
| 欄 | 操作 | 編集中の文字列 |
|---|
| (0,0) | 初期状態 | |saka |
|
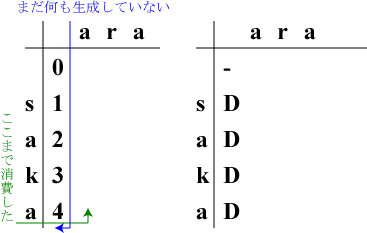 |
左表の最左の行の欄(L,0)に削除のコストを足しながら記入していきます。
「削除」ですから右表の(L,0)には"D"と記入します。
| 欄 | 操作 | 編集中の文字列 |
|---|
| (0,0) | 初期状態 | |saka |
| (1,0) | 's'を『削除』 | |aka |
| (2,0) | 'a'を『削除』 | |ka |
| (3,0) | 'k'を『削除』 | |a |
| (4,0) | 'a'を『削除』 | | |
|
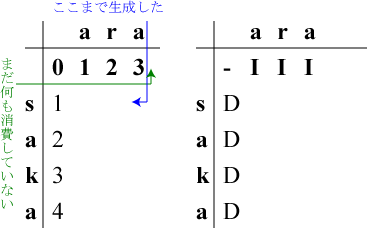 |
左表の最上の行の欄(0,R)に挿入のコストを足しながら記入していきます。
「挿入」ですから右表の(0,R)には"I"と記入します。
| 欄 | 操作 | 編集中の文字列 |
|---|
| (0,0) | 初期状態 | |saka |
| (0,1) | 'a'を『挿入』 | a|saka |
| (0,2) | 'r'を『挿入』 | ar|saka |
| (0,3) | 'a'を『挿入』 | ara|saka |
|
 |
左表の(L,R)に記入すべきコストは
- (L-1,R-1)の状態からの「置換」
- (L-1,R-1)の状態からの「カーソル移動」←文字が等しい場合だけ
- (L-1,R)の状態からの「削除」
- (L,R-1)の状態からの「挿入」
のどれかです。最小のコストを計算して左表に記入します。
右表の(L,R)には選んだ操作を記入します。
|
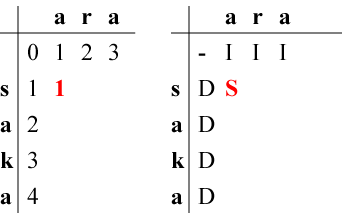 |
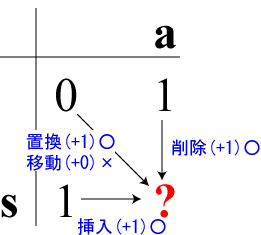
左表の(1,1)の状態に到達する最小コストを考えます。
カーソル位置にある文字's'と生成したい文字'a'が等しくないので
「(0,0)の状態からの『カーソル移動』」は使えません。
したがって、(1,1)に到達するには
- 「(0,0)の状態から's'を'a'に『置換』」、コストは 0+1=1
- 「以前に'a'を『挿入』した(0,1)の状態からの's'の『削除』」、コストは1+1=2
- 「以前に's'を『削除』した(1,0)の状態からの'a'の『挿入』」、コストは1+1=2
という3種類の方法がありえることがわかります。
そのうち「(0,0)の状態から's'を'a'に『置換』」が最小コストで1なので、
左表(1,1)には1、右表(1,1)にはS (置換, Substitute)を記入します。
| 欄 | 操作 | 編集中の文字列 |
|---|
| (0,0) | 初期状態 | |saka |
| (1,1) | 's'を'a'に『置換』 | a|aka |
欄(1,1)の状態は、操作の順番はともかく
「『消費すべき文字列』から先頭の's'が無くなり、
『生成すべき文字列』から先頭の'a'が無くなった」状態です。
その状態にたどり着くための編集操作の最小コストが1であったわけです。
|
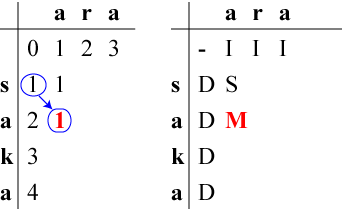 |
左表の(2,1)は、カーソル位置にある『消費すべき』文字と
これから『生成すべき文字』がどちらも'a'なのでMatchしますから
「(1,0)の状態からの『カーソル移動』」が使えます。
他にも「(1,1)の状態から'a'を『削除』」
「(2,0)の状態から'a'を『挿入』」という
方法が使えますが、左表の(2,1)に到達するには
「(1,0)の状態からの『カーソル移動』」が最小コストです。
左表(2,1)には1+0=1を、
右表(2,1)にはM (カーソル移動, Match)を記入します。
| 欄 | 操作 | 編集中の文字列 |
|---|
| (1,0) | 's'を『削除』 | |aka |
| (2,1) | 同じ'a'なので『カーソル移動』 | a|ka |
欄(2,1)の状態は、「まず『消費すべき文字列』から先頭の's'を『削除』し、
その次に『消費すべき文字列』と『生成すべき文字列』がともに'a'であったので
『カーソル移動』した」状態です。
その状態にたどり着くための演習操作の最小コストが「削除(コスト1)」と
「カーソル移動(コスト0)」の合計で、1です。
|
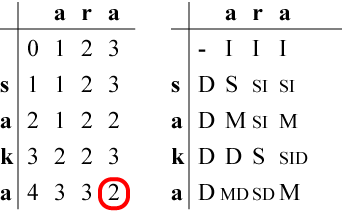 |
表を全て記入した状態です。
右表の中で複数の記号が併記されている場合はどちらの操作でも
最小コストになることを表しています。
たとえば"SI"という記号は「置換または挿入のどちらの操作でもOK」
の意味です。
左表の最右下の欄である(4,3)を見ることで最小コストは2であることがわかります。
|
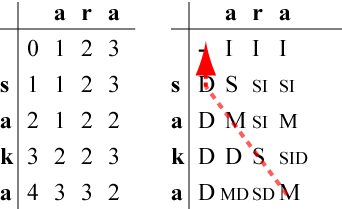 |
最小コストに到達する手段は、右表の右下の欄からスタートして、
操作を逆に
- SかMならば置換かカーソル移動によってその欄に到達したので、左上へ
- Iならば挿入によってその欄に到達したので、左へ
- Dならば削除されてその欄に到達したので、上へ
と辿ればわかります。
最小コストの操作手順は以下のようになります。
| 欄 | 操作 | 編集中の文字列 |
|---|
| (0,0) | 初期状態 | |saka |
| (1,0) | 's'を『削除』 | |aka |
| (2,1) | 'a'は『カーソル移動』 | a|ka |
| (3,2) | 'k'を'r'に『置換』 | ar|a |
| (4,3) | 'a'は『カーソル移動』 | ara| |
|
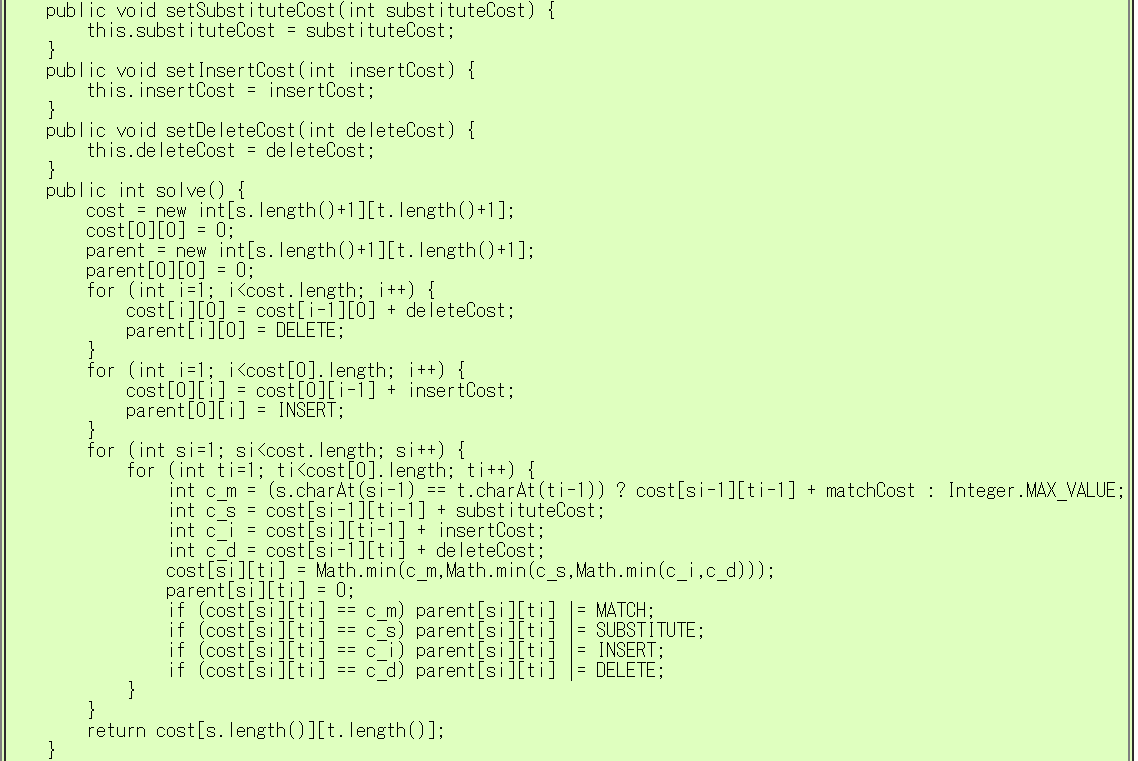
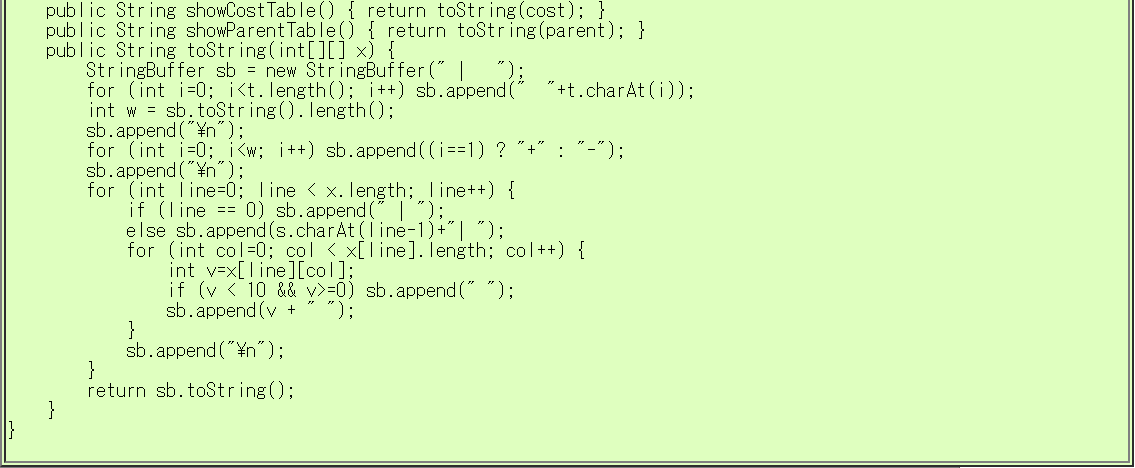
編集距離を計算するプログラム例
2つの文字列の編集距離を計算するプログラムを考えましょう。
次のプログラムでは、配列 cost に「それぞれの状態に至る最小コスト」を記録し、
配列 parent に「その状態に最小コストで到達するための直近の操作」を記録します。
操作を種類毎に異なるbitで表現しているので、複数の操作でも同時に記録できます。
- MATCH ... 最も右の 1bit (= 1)
- SUBSTITUTE ... 右から2番目のbit (= 2)
- INSERT ... 右から3番目のbit (= 4)
- DELETE ... 右から4番目のbit (= 8)
たとえば手順が SI (SUBSTITUTEまたはINSERT)の場合は 2+4で
6と記録されます。
簡単のため、最小コストの編集手順はたとえ複数存在しても
一通りだけ表示するようにしています。


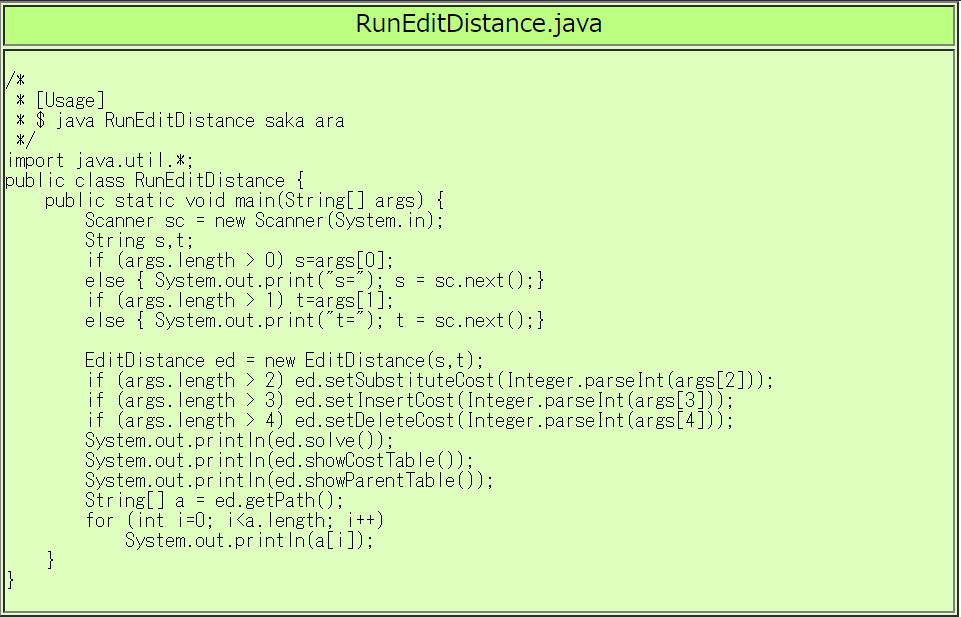
| RunEditDistance.javaの実行例 |
$ javac RunEditDistance.java EditDistance.java
$ java RunEditDistance "saka" "ara"
2
| a r a
-+------------
| 0 1 2 3
s| 1 1 2 3
a| 2 1 2 2
k| 3 2 2 3
a| 4 3 3 2
| a r a
-+------------
| 0 4 4 4
s| 8 2 6 6
a| 8 1 6 1
k| 8 8 2 14
a| 8 9 10 1
delete 's'
matches 'a' and 'a'
substitute 'k' by 'r'
matches 'a' and 'a'
$ java RunEditDistance "apple is good" "applet is god"
2
| a p p l e t i s g o d
-+------------------------------------------
| 0 1 2 3 4 5 6 7 8 9 10 11 12 13
a| 1 0 1 2 3 4 5 6 7 8 9 10 11 12
p| 2 1 0 1 2 3 4 5 6 7 8 9 10 11
p| 3 2 1 0 1 2 3 4 5 6 7 8 9 10
l| 4 3 2 1 0 1 2 3 4 5 6 7 8 9
e| 5 4 3 2 1 0 1 2 3 4 5 6 7 8
| 6 5 4 3 2 1 1 1 2 3 4 5 6 7
i| 7 6 5 4 3 2 2 2 1 2 3 4 5 6
s| 8 7 6 5 4 3 3 3 2 1 2 3 4 5
| 9 8 7 6 5 4 4 3 3 2 1 2 3 4
g| 10 9 8 7 6 5 5 4 4 3 2 1 2 3
o| 11 10 9 8 7 6 6 5 5 4 3 2 1 2
o| 12 11 10 9 8 7 7 6 6 5 4 3 2 2
d| 13 12 11 10 9 8 8 7 7 6 5 4 3 2
| a p p l e t i s g o d
-+------------------------------------------
| 0 4 4 4 4 4 4 4 4 4 4 4 4 4
a| 8 1 4 4 4 4 4 4 4 4 4 4 4 4
p| 8 8 1 5 4 4 4 4 4 4 4 4 4 4
p| 8 8 9 1 4 4 4 4 4 4 4 4 4 4
l| 8 8 8 8 1 4 4 4 4 4 4 4 4 4
e| 8 8 8 8 8 1 4 4 4 4 4 4 4 4
| 8 8 8 8 8 8 2 1 4 4 5 4 4 4
i| 8 8 8 8 8 8 10 10 1 4 4 4 4 4
s| 8 8 8 8 8 8 10 10 8 1 4 4 4 4
| 8 8 8 8 8 8 10 1 8 8 1 4 4 4
g| 8 8 8 8 8 8 10 8 10 8 8 1 4 4
o| 8 8 8 8 8 8 10 8 10 8 8 8 1 4
o| 8 8 8 8 8 8 10 8 10 8 8 8 9 2
d| 8 8 8 8 8 8 10 8 10 8 8 8 8 1
matches 'a' and 'a'
matches 'p' and 'p'
matches 'p' and 'p'
matches 'l' and 'l'
matches 'e' and 'e'
insert 't'
matches ' ' and ' '
matches 'i' and 'i'
matches 's' and 's'
matches ' ' and ' '
matches 'g' and 'g'
delete 'o'
matches 'o' and 'o'
matches 'd' and 'd'
$ java RunEditDistance "thou shalt not" "you should not"
5
| y o u s h o u l d n o t
-+---------------------------------------------
| 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
t| 1 1 2 3 4 5 6 7 8 9 10 11 12 13 13
h| 2 2 2 3 4 5 5 6 7 8 9 10 11 12 13
o| 3 3 2 3 4 5 6 5 6 7 8 9 10 11 12
u| 4 4 3 2 3 4 5 6 5 6 7 8 9 10 11
| 5 5 4 3 2 3 4 5 6 6 7 7 8 9 10
s| 6 6 5 4 3 2 3 4 5 6 7 8 8 9 10
h| 7 7 6 5 4 3 2 3 4 5 6 7 8 9 10
a| 8 8 7 6 5 4 3 3 4 5 6 7 8 9 10
l| 9 9 8 7 6 5 4 4 4 4 5 6 7 8 9
t| 10 10 9 8 7 6 5 5 5 5 5 6 7 8 8
| 11 11 10 9 8 7 6 6 6 6 6 5 6 7 8
n| 12 12 11 10 9 8 7 7 7 7 7 6 5 6 7
o| 13 13 12 11 10 9 8 7 8 8 8 7 6 5 6
t| 14 14 13 12 11 10 9 8 8 9 9 8 7 6 5
| y o u s h o u l d n o t
-+---------------------------------------------
| 0 4 4 4 4 4 4 4 4 4 4 4 4 4 4
t| 8 2 6 6 6 6 6 6 6 6 6 6 6 6 1
h| 8 10 2 6 6 6 1 4 4 4 4 4 4 4 4
o| 8 10 1 6 6 6 14 1 4 4 4 4 4 5 4
u| 8 10 8 1 4 4 4 12 1 4 4 4 4 4 4
| 8 10 8 8 1 4 4 4 12 2 6 1 4 4 4
s| 8 10 8 8 8 1 4 4 4 4 6 14 2 6 6
h| 8 10 8 8 8 8 1 4 4 4 4 4 4 6 6
a| 8 10 8 8 8 8 8 2 6 6 6 6 6 6 6
l| 8 10 8 8 8 8 8 10 2 1 4 4 4 4 4
t| 8 10 8 8 8 8 8 10 10 10 2 6 6 6 1
| 8 10 8 8 9 8 8 10 10 10 10 1 4 4 4
n| 8 10 8 8 8 8 8 10 10 10 10 8 1 4 4
o| 8 10 9 8 8 8 8 1 14 10 10 8 8 1 4
t| 8 10 8 8 8 8 8 8 2 14 10 8 8 8 1
delete 't'
substitute 'h' by 'y'
matches 'o' and 'o'
matches 'u' and 'u'
matches ' ' and ' '
matches 's' and 's'
matches 'h' and 'h'
insert 'o'
substitute 'a' by 'u'
matches 'l' and 'l'
substitute 't' by 'd'
matches ' ' and ' '
matches 'n' and 'n'
matches 'o' and 'o'
matches 't' and 't'
|
アルゴリズムc 演習
作成したプログラムが正しく動作することを確認したら、それぞれの
提出先に提出しなさい。
提出した後は、正しく提出されていることを
http://ynitta.com/class/algoC/local/handin/
で必ず確認しておいて下さい。
課題提出〆切は次回の講義の開始時刻です。
課題8a
Substitute, Insert, Delete, Matchそれぞれの
文字列操作のコストが1,1,1,0であるとする。
文字列
"sushi and wine belong to food"
を編集して文字列
"sun shines and window blows, good"
を生成する場合の最小コストを求めよ。
課題8b
| 提出ファイル | NearWord.java |
|---|
| コメント欄:
|
学生ごとに入力データセットが異なるので注意が必要である。
学生番号の末尾の数字を3で割った余りで入力データセットが割り当てられる。
割り当てられたデータをプログラムで処理した結果の出力をコメント欄に貼り付けておくこと。
(1度に1個の入力データを処理した、合計7回分の実行結果を貼り付けること)。
| 余りが0の人(gxxxx[0369]) | 余りが1の人(gxxxx[147]) | 余りが2の人(gxxxx[258]) |
|---|
abcense
explasion
foorin
irerebant
nowlege
rigitemite
newclear
|
akcept
exagelat
forine
embaras
misaile
gaard
okacionally
|
colligion
forhedd
riblaly
haight
hipoksicy
laiing
brouchere
|
|
|---|
| 提出先: |
「宿題提出Web:アルゴリズムc:課題8b」
http://ynitta.com/class/algoC/local/handin/up.php?id=kadai8b
|
|---|
「英単語のタイプミスを指摘し、正しい単語の候補を示す」プログラムを作りなさい。
ただし、以下の仕様を満たすこと。
- ユーザの入力は1行とする。途中に空白文字を含んでもよい。
- 辞書として mwords_74550common.txt を用いる。
- 「ユーザが入力した行」と最も編集距離が近い「辞書中の行」を発見すること。
- 出力の最初の行が「最小の編集距離」、
2行目以降は「最も編集距離が短い行の内容」であること。
- 解が複数ある場合は、全ての解を1行に1つずつ表示すること。
-
文字列操作
Substitute, Insert, Delete, Match
のコストはそれぞれ1,1,1,0とする。
"mwords_74550common.txt"の内容は
Grady Ward's Moby Project
http://icon.shef.ac.uk/Moby/mwords.html
から入手できる単語のリストのうちの "74550com.mon"
(複数の辞書に含まれる一般的な単語 74550 語)である。
| mwords_74550common.txtの内容(抜粋) |
alow
alp
alpaca
alpenglow
alpenhorn
alpenstock
alpestrine
alpha
alpha and omega
alpha decay
|
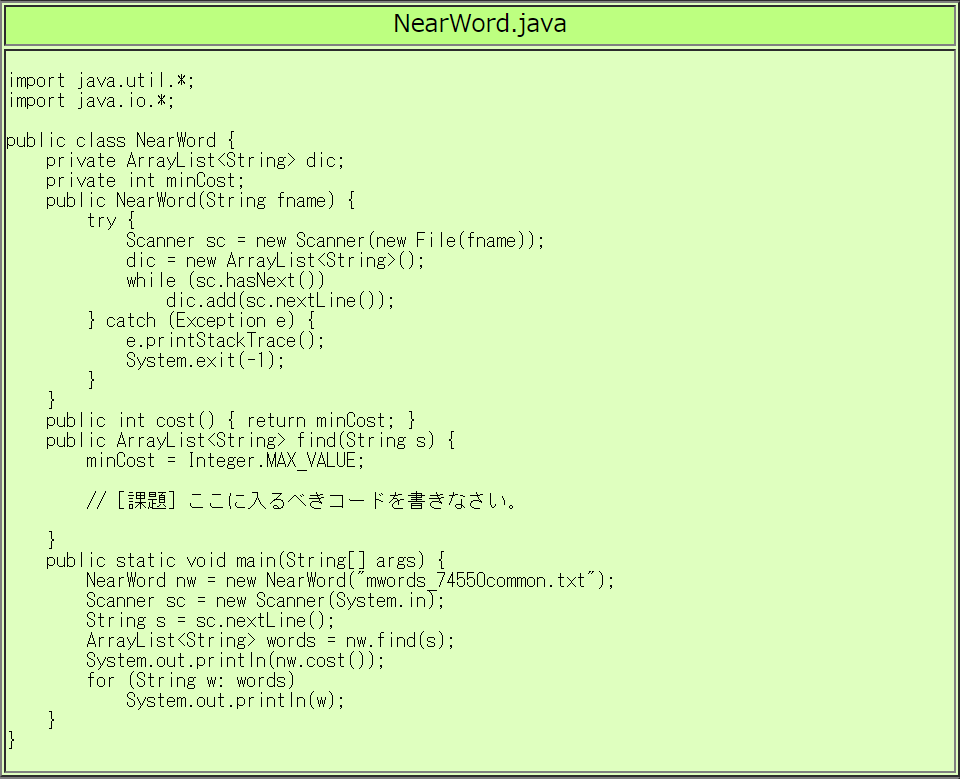
| NearWord.javaの実行例 |
$ javac NearWord.java
$ java NearWord
Amanda's applet
5
Adam's apple
$ java NearWord
womin
1
woman
women
$ java NearWord
thiatar
2
theater
$ java NearWord
the Internet
6
eterne
herb bennet
interne
internee
phenanthrene
tenter
theater
theatre
|
課題8c
次の問題を解くプログラム SquareDP.javaを作成しなさい。
ただし、一辺の長さを n として O(n2)のアルゴリズムを使うこと。
問題
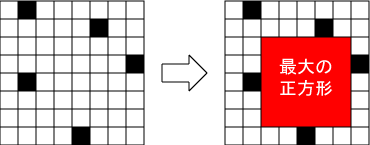
「白いタイル」と「黒いタイル」がぎっしりと敷き詰められた長方形の領域を考える。
「白いタイル」だけから構成された最も大きな正方形領域を探すプログラムを
作成しなさい。
入力は複数のデータセットからなる。
データセットの終わりは2個の0で表される。
Dataset1
Dataset2
...
0 0
各データセットは以下の形式から成る。
L C
T1,1 T1,2 T1,3 ... T1,C
T2,1 T2,2 T2,3 ... T2,C
...
TL,1 TL,2 TL,3 ... TL,C
LとCは1以上1000以下の整数であり、それぞれ部屋の中の縦方向と横方向の
タイル数を表している。
Ti,jはタイルの状態を表現する整数であり、次の意味を持つ
各データセットに対し、その中に取れる最も大きな白い正方形領域を
見つけ、正方形の1辺の長さを出力すること。
各データセットに対する答を出力する際は改行し、
1行につき答となる1個の整数を含んだ1行を出力すること。
| サンプル入力 |
4 6
0 0 0 0 0 1
1 0 0 0 1 0
0 0 0 0 0 0
0 0 0 0 0 1
6 6
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
8 8
1 0 0 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0
|
ヒント
単純に考えるとこれは O(n5)の計算量が必要となる
(全てのタイルについて繰り返すのにO(n2)。
そこを左上隅とする正方形の長さを1から増やしていくのにO(n)。
x方向とy方向それぞれにその大きさの正方形が取れることを
確認するのにO(n2)なので)。
これに対し、次のようにDPで考えるとO(n2)で計算できる。
白い各タイルについて、「そのタイルを右下隅とする最大の正方形の大きさ」
をf(line,col)とすると、
f(line,col)=min( f(line-1,col-1), f(line-1,col), f(line,col-1)) + 1
という関係が成り立つ。
黒い各タイルについては、そもそも正方形が置けないので f(line,col)=0 である。
最上辺と最左辺のタイルはそれぞれ「白ならば1,黒ならば0」と初期化できる。
すなわち
line=0 または col=0の場合
f(line, col) = 1 (タイルが白の場合)
f(line, col) = 0 (タイルが黒の場合)
全てのタイルについてf(line,col)を計算してその最大値を見つければいいが、
タイルの総数はO(n2)なので、全体の計算量もO(n2)
となる。