アルゴリズムc 第7回

動的計画法

ダイナミックプログラミング (Dynamic Programming, 動的計画法) とは、 最適化問題を解くために有効なアルゴリズムです。

n種類(整数個)の要素に関する最適解を求めるのに、 まず1種類の要素だけが使えるものとして、解を表に入れていきます。 そのあと、別の要素をもう1種類だけ追加して、表の値がどう変化するか を調べます。 それが終わると、また別の要素を1種類だけ追加して、表の値が どう変化するかを調べます。 このように要素を順に追加していき、全部の要素を追加し終った後の 表の状態で最適解がわかるというわけです。

具体例を見た方がわかりやすいので、次のナップザック問題を使って 動的計画法を説明します。

ナップザック問題

N種類の品物 Ai (ただし 1≦i≦n)の 「価格, Ai.value」と「大きさ, Ai.size」 が与えられた状態で、 大きさsの袋に品物をきっちり詰めたときの 「詰めた品物の価格の最大値」を求める問題です。

たとえば、次の表のような5種類の品物を適当にまぜて、 ある大きさの袋にきっちり詰めたときに、 合計価格の最大値がいくらになるかを考える問題が相当します。 ただし、品物1種類につき使える個数に制限がある場合と、 制限がない(同じものを何個でも詰めていい)場合があります。

品物
品番名前大きさ価格
0orange22
1apple34
2grape57
3peach711
4melon914

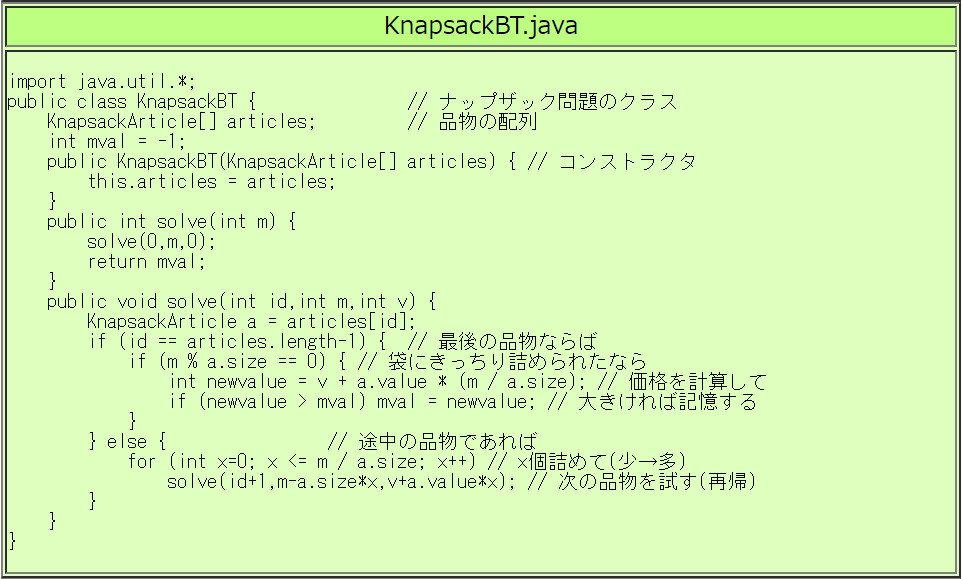
参考: ナップザック問題をバックトラック法で解いてみる

個数制限がある場合

どの品物も最大1個までしか使えない場合を考えてみましょう。

この場合はどの品物に関しても「使う or 使わない」のどちらかを 選ぶしかないわけですから、n個の品物があるときは 2n通りの組合せが考えられます。 Java風のアルゴリズムで表すと次のようになります。

ナップザック問題をバックトラックアルゴリズム(Java風)で書いた場合
    // int[] aは品物の配列
    // int s は袋のサイズ
    // int vmax は価格の最大値
    for (x0=0; x0 <= 1; x0++) {  // 品物A1
        int s1 = s - a[0].size * x0;
        for (x1=0; x1 <= 1; x1++) {  // 品物A2
          int s2 = s1 - a[1].size * x1;
             ...

              for(xn-1=0; xn-1 <= 1; xn-1++) { // 品物An-1
                 if (sn-1 - a[n-1].size * xn-1 == 0) {  // 袋にいっぱいならば
                   int v = a[0].value * x0 + a[1].value * x1
                          + ... + a[n-1].value * xn-1;  // 価格を計算して
                   if (vmax < v) vmax = v;  // 最大価格の更新
                 }
              }
          
        }
    }

個数制限がない場合

バックトラックで求めようとすると、 品物Ai(,ただし1≦i≦n)に関して、 「Aiの大きさ」を Ai.size 「Aiの価格」を Ai.value とすると 

      n
s ＝ Σ Ai.size × xi 
     i=1
となる Aviを繰り返しによって求めて、そのときの 
      n
s ＝ Σ Avi.value × xi 
     i=1
を計算して最大値を求めることになります。 Java風のアルゴリズムで表すと次のようになります。

ナップザック問題をバックトラックアルゴリズム(Java風)で書いた場合
    // int[] aは品物の配列
    // int s は袋のサイズ
    // int vmax は価格の最大値
    for (x0=0; x0 <= s /a[0].size; x0++) {  // 品物A1
        int s1 = s - a[0].size * x0;
        for (x1=0; x1 <= s1 / a[1].size; x1++) {  // 品物A2
          int s2 = s1 - a[1].size * x1;
             ...

              for(xn-1=0; xn-1 <= sn-1 / a[n-1].size; xn-1++) { // 品物An-1
                 if (sn-1 - a[n-1].size * sn-1 == 0) {  // 袋にいっぱいならば
                   int v = a[0].value * x0 + a[1].value * x1
                          + ... + a[n].value * xn;  // 価格を計算して
                   if (vmax < v) vmax = v;  // 最大価格の更新
                 }
              }
          
        }
    }

品物の種類を n, 袋の大きさをmとすると、バックトラック法では 計算は各品物について(m / 品物のサイズ)回必要で、 これをバックトラックしながらn段に渡って再帰呼び出ししますから 全体で(m / 品物のサイズ)n回の計算が必要です。 計算量は O (mn) となります。

下の実行例では m=500で 0.84秒、m=1000で10.44秒, m=2000で158秒と急激に実行時間が増えていることがわかります。

さらに、n (品物の種類)を増やした場合は指数オーダーで計算時間は増加するので、 たとえば n=20, m=500 程度でもとても現実に計算するのは不可能な計算 となってしまいます。 



















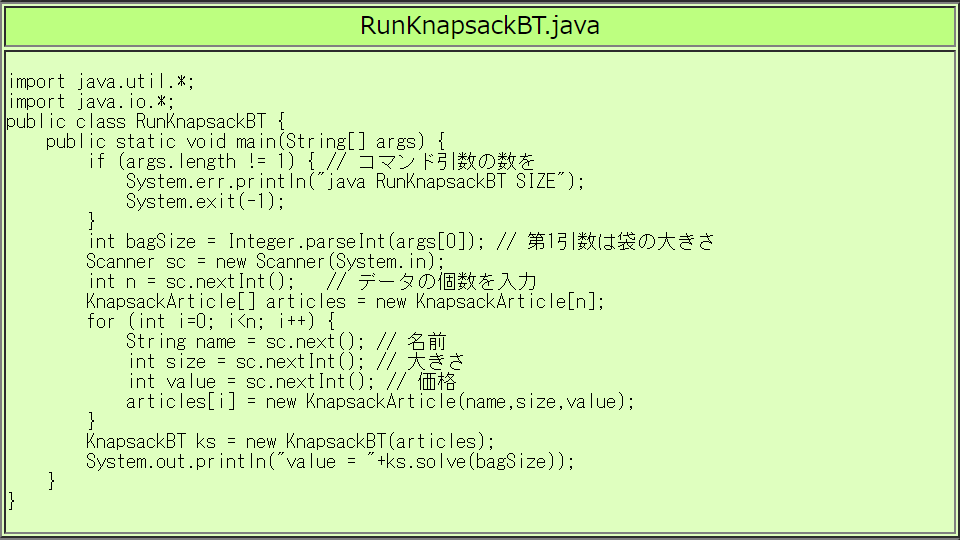
RunKnapsackBT.javaの実行例
% javac KnapsackBT.java RunKnapsackBT.java 
% time (java RunKnapsackBT 500 < knapsack01.txt)    timeコマンドで実行時間を測る
value = 785

real    0m0.373s  ← 0.373秒かかった
user    0m0.015s
sys     0m0.031s
% time (java RunKnapsackBT 1000 < knapsack01.txt)  
value = 1571

real    0m2.756s  ← 2.756秒かかった
user    0m0.015s
sys     0m0.015s
% time (java RunKnapsackBT 2000 < knapsack01.txt)  
value = 3142

real    0m37.638s  ← 37.638秒かかった
user    0m0.015s
sys     0m0.015s






knapsack01.txt
5
orange 2 2
apple 3 4
grape 5 7
peach 7 11
melon 9 14






knapsack02.txt
8
lemon 3 2
orange 7 5
apple 11 9
peach 17 15
pear 19 17
grape 23 21
pine 29 27
melon 31 28





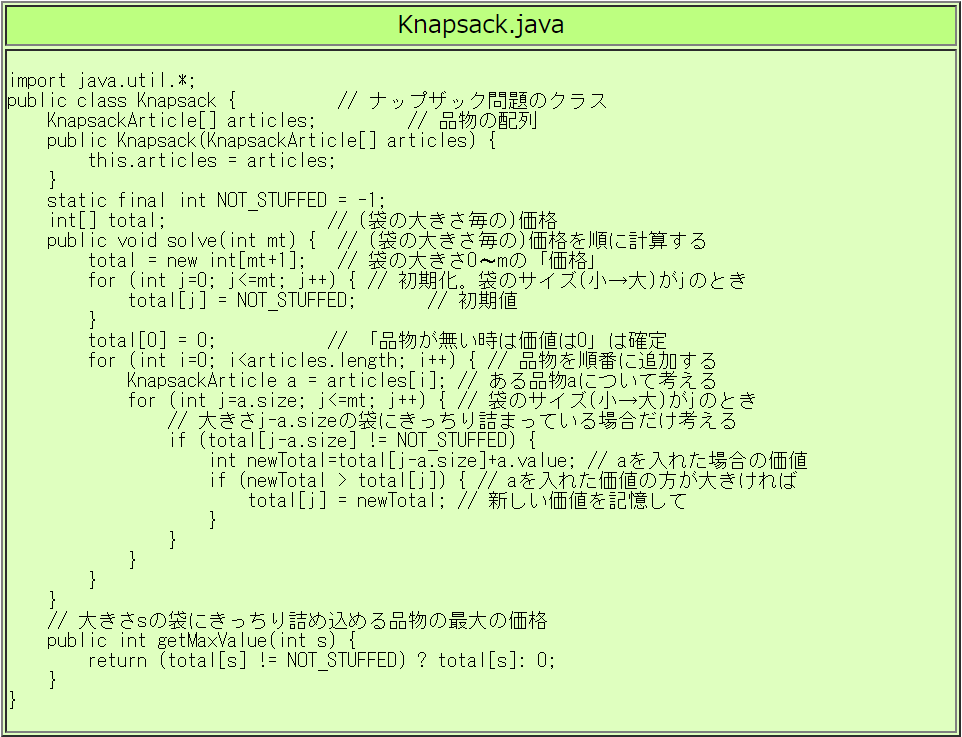
ナップザック問題(個数制限あり)を動的計画法で解く




動的計画法は、

    

  1. まず、少ない種類の要素で問題を解き、解いた結果を表として保存する。
    2. 

  2. kに関して以下の操作を全種類になるまで繰り返す。
    3. 
  


というものです。





品物が1個ずつしか使えないナップザック問題を考えます。





以下では、
品物0〜iだけを使って大きさsの袋にきっちりと詰め込むナップザック問題の
解を、袋の大きさsの関数として fi(s) と記述しています。





まず、使える品物が何もない初期状態を考えます。
すなわち、袋の大きさ=0で価値=0です。





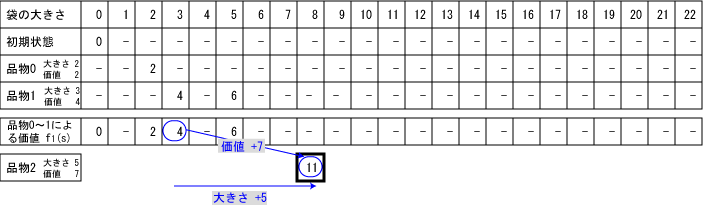
これを使って、品物0が使えるようになった場合の計算を行います。
大きさsの袋に品物をきっちり詰め込めた時の最大価値
f0(s) を表にします。





次に、品物1が新たに使えるようになったとして、f0(s)
を参照しながらf1(s)を求めます。





品物0〜1が使える場合のf1(s)が求まった状態で、
新たに品物2が使えるようになった場合の計算を表したのが
次の図です。
大きさs=8の袋に品物2を詰め込む場合は、f1(3)
すなわち f1(s - 品物2の大きさ)
を参照して計算しています。









すなわち、品物i+1の大きさをsizei+1、価値をValuei+1
とすると

    fi(s - sizei+1) + Valuei+1
と
    fi(s)


を比較して、大きい方をfi+1(s)とすればよいのです。





実際にプログラミングするときは次のようにするとよいでしょう。
 






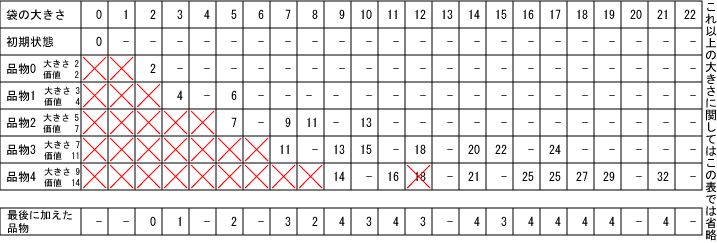
品物を0種類から始めて、品物の種類を1つずつ増やしていき、
品物全部について表を完成させると次のようになります。









ナップザック問題(個数制限なし)を動的計画法で解く




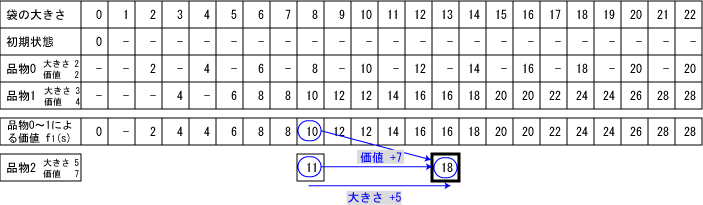
品物が何個でも使えるナップザック問題を考えます。







f1(s)を参照しながら、品物2も使える場合の計算を
している様子が次の図です。
大きさs=13の袋に品物2を詰め込む場合は、f1(8)
すなわち f1(s - 品物2の大きさ)
を参照して計算しています。
ただし、この場合は品物2を複数個使ってもいいわけですから
「品物2も使った場合の最大値」である f2(8)も
参照する必要があります。








式で表すと次のように説明できます。





すなわち、同じ品物が何個も使える問題では

    fi+1(s - sizei+1) + Valuei+1
と
    fi(s)


を比較して、大きい方をfi+1(s)とすればよいのです。






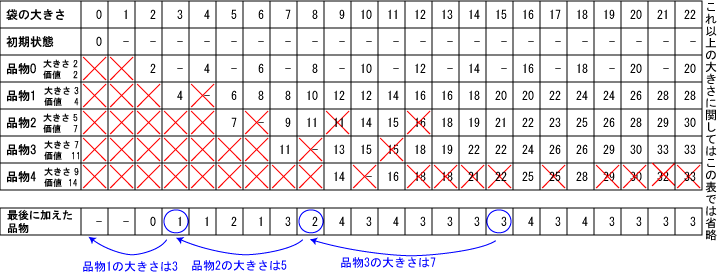
品物を0種類から始めて、品物の種類を1つずつ増やしていき、
品物全部について表を完成させると次のようになります。
「その結果を得るために最後に加えた品物」も別に管理しておけば、
その結果を得るために必要な各品物を求めることができます。





また、「その結果を得るために最後に加えた品物」も記憶しておけば、
その最適解を得るために必要な要素(品物)もわかります。









品物の種類を n, 袋の大きさをmとすると、
動的計画法では計算は各品物についてm回必要で(表を小さい方から大きい方へ)、
それを品物の種類nだけ繰り返しますから、計算量は O (m×n) となります。






下の実行例では m=500で 0.09秒、m=1000でもm=2000でも 0.11秒と、
もともと高速であり、しかも mを増やしても実行時間はゆっくりと
しか増えないことがわかります。





品物の種類 n を増やしたときでさえ、計算時間はゆっくりとしか増えていきません。





















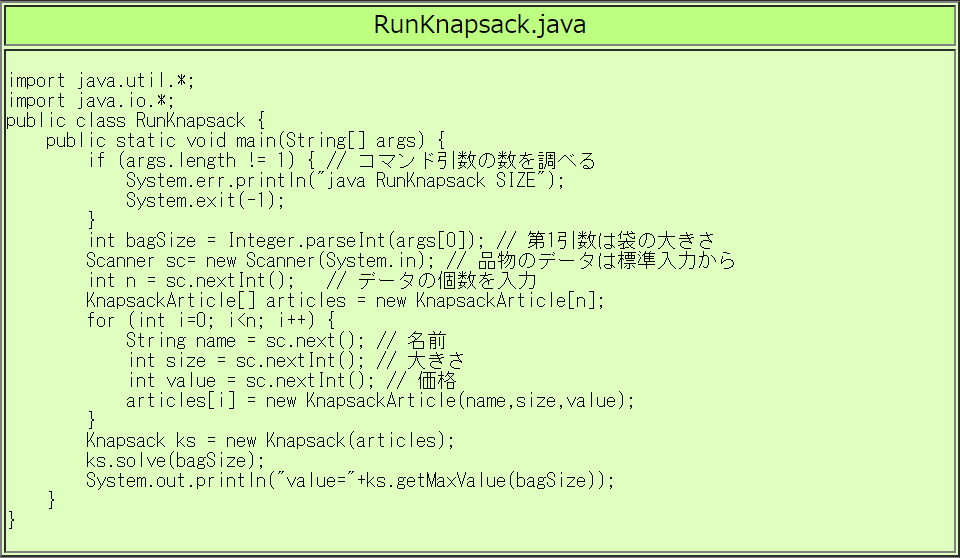
RunKnapsack.javaの実行例
% javac RunKnapsack.java Knapsack.java 
% time (java RunKnapsack 500 < knapsack01.txt)    timeコマンドで実行時間を測る
value=785

real    0m0.206s  ← 0.206秒かかった
user    0m0.015s
sys     0m0.015s
% time (java RunKnapsack 1000& < knapsack01.txt)  
value=1571

real    0m0.197s  ← 0.197秒かかった
user    0m0.015s
sys     0m0.031s
% time (java RunKnapsack 2000 < knapsack01.txt)  
value=3142

real    0m0.221s  ← 0.221秒かかった
user    0m0.046s
sys     0m0.015s



選んだ品物の表示




選んだ品物を表示するように変更してみましょう。





「ある袋の大きさに対して、最大の価値を更新する場合は、
最後に追加した品物を記憶しておく」ことで追加した品物を
たどることができます。




KnapsackChoice.javaの変更点
*** java/Knapsack.java	Tue Jun  9 15:30:30 2020
--- java/KnapsackChoice.java	Mon Apr  8 15:53:16 2019
***************
*** 1,15 ****
  import java.util.*;
! public class Knapsack {          // ナップザック問題のクラス
      KnapsackArticle[] articles;         // 品物の配列
!     public Knapsack(KnapsackArticle[] articles) {
  	this.articles = articles;
      }
      static final int NOT_STUFFED = -1;
      int[] total;                // (袋の大きさ毎の)価格
      public void solve(int mt) {  // (袋の大きさ毎の)価格を順に計算する
          total = new int[mt+1];   // 袋の大きさ0〜mの「価格」
          for (int j=0; j<=mt; j++) { // 初期化。袋のサイズ(小→大)がjのとき
              total[j] = NOT_STUFFED;       // 初期値
          }
  	total[0] = 0;		// 「品物が無い時は価値は0」は確定
          for (int i=0; i<articles.length; i++) { // 品物を順番に追加する
--- 1,18 ----
  import java.util.*;
! public class KnapsackChoice {          // ナップザック問題のクラス
      KnapsackArticle[] articles;         // 品物の配列
!     public KnapsackChoice(KnapsackArticle[] articles) {
  	this.articles = articles;
      }
      static final int NOT_STUFFED = -1;
      int[] total;                // (袋の大きさ毎の)価格
+     int[] choice;               // (袋の大きさ毎の)最後に選んだ品物
      public void solve(int mt) {  // (袋の大きさ毎の)価格を順に計算する
          total = new int[mt+1];   // 袋の大きさ0〜mの「価格」
+         choice = new int[mt+1];  // 袋の大きさ0〜mの「最後に選んだ品物」
          for (int j=0; j<=mt; j++) { // 初期化。袋のサイズ(小→大)がjのとき
              total[j] = NOT_STUFFED;       // 初期値
+             choice[j] = NOT_STUFFED; // 選んだ品物は無い(空っぽ)
          }
  	total[0] = 0;		// 「品物が無い時は価値は0」は確定
          for (int i=0; i<articles.length; i++) { // 品物を順番に追加する
***************
*** 20,25 ****
--- 23,29 ----
  		    int newTotal=total[j-a.size]+a.value; // aを入れた場合の価値
  		    if (newTotal > total[j]) { // aを入れた価値の方が大きければ
  			total[j] = newTotal; // 新しい価値を記憶して
+ 			choice[j] = i; // aを加えたことを記録する
  		    }
  		}
  	    }
***************
*** 29,32 ****
--- 33,47 ----
      public int getMaxValue(int s) {
  	return (total[s] != NOT_STUFFED) ? total[s]: 0;
      }
+     // 選んだ品物をベクタとして返す
+     public ArrayList<KnapsackArticle> getArticles(int s) {
+ 	ArrayList<KnapsackArticle> v = new ArrayList<KnapsackArticle>();
+ 	while (s > 0) {		// 袋の大きさsが0になるまで
+ 	    int id = choice[s];	// 「最後に選んだ品物の番号」を取り出して
+ 	    KnapsackArticle a = articles[id]; // 最後に選んだ品物を取り出して
+ 	    v.add(a); // 記録する
+ 	    s -= a.size;	// 袋の大きさ-=「最後に選んだ品物」の大きさ
+ 	}
+ 	return v;
+     }
  }






RunKnapsackChoice.javaの変更点
*** java/RunKnapsack.java	Tue Jun  9 15:33:42 2020
--- java/RunKnapsackChoice.java	Tue Jun  9 15:33:48 2020
***************
*** 1,9 ****
  import java.util.*;
  import java.io.*;
! public class RunKnapsack {
      public static void main(String[] args) {
  	if (args.length != 1) {	// コマンド引数の数を調べる
! 	    System.err.println("java RunKnapsack SIZE");
  	    System.exit(-1);
  	}
  	int bagSize = Integer.parseInt(args[0]); // 第1引数は袋の大きさ
--- 1,9 ----
  import java.util.*;
  import java.io.*;
! public class RunKnapsackChoice {
      public static void main(String[] args) {
  	if (args.length != 1) {	// コマンド引数の数を調べる
! 	    System.err.println("java RunKnapsackChoice SIZE");
  	    System.exit(-1);
  	}
  	int bagSize = Integer.parseInt(args[0]); // 第1引数は袋の大きさ
***************
*** 16,23 ****
  	    int value = sc.nextInt(); // 価格
  	    articles[i] = new KnapsackArticle(name,size,value);
  	}
! 	Knapsack ks = new Knapsack(articles);
  	ks.solve(bagSize);
  	System.out.println("value="+ks.getMaxValue(bagSize));
      }
  }
--- 16,27 ----
  	    int value = sc.nextInt(); // 価格
  	    articles[i] = new KnapsackArticle(name,size,value);
  	}
! 	KnapsackChoice ks = new KnapsackChoice(articles);
  	ks.solve(bagSize);
  	System.out.println("value="+ks.getMaxValue(bagSize));
+ 	ArrayList<KnapsackArticle> v = ks.getArticles(bagSize);
+ 	String s="";
+ 	for (int i=0; i<v.size(); i++) s += v.get(i) + " ";
+ 	System.out.println(s);
      }
  }






RunKnapsackChoice.javaの実行例
% javac RunKnapsackChoice.java KnapsackChoice.java 
% java RunKnapsackChoice 20 < knapsack01.txt 
value=30
[peach,7,11] [peach,7,11] [apple,3,4] [apple,3,4] 
% java RunKnapsackChoice 50 < knapsack01.txt 
value=78
[melon,9,14] [melon,9,14] [melon,9,14] [melon,9,14] [peach,7,11] [peach,7,11] 








補足1



今回解説したのは、「袋にきっちり詰めるナップザック」の問題ですが、
「袋に空間があっても構わない」問題も同様な方法で解くことができます。




「袋にきっちり詰めるナップザック」の問題における
「袋の大きさsの時の解」を f(s) と書くことにすると
「袋に空間があっても構わない」問題では「1≦i≦sにおけるf(i)の最大値」
が解となります。











アルゴリズムc 演習






作成したプログラムが正しく動作することを確認したら、それぞれの
提出先に提出しなさい。





提出した後は、正しく提出されていることを

http://ynitta.com/class/algoC/local/handin/

で必ず確認しておいて下さい。





課題提出〆切は次回の講義の開始時刻です。




課題7a





提出ファイルKnapsackChoice.java


コメント欄:knapsack02.txtを入力としたとき、袋の大きさ112でのRunKnapsackChoice.javaの出力


提出先:
「宿題提出Web:アルゴリズムc：課題7a」

http://ynitta.com/class/algoC/local/handin/up.php?id=kadai7a








RunKnapsackChoice.javaを動作させて下さい。








課題7b





提出ファイルDPSum.java


コメント欄:dpsum02.txtを入力としたとき、RunDPSum.javaの出力


提出先:
「宿題提出Web:アルゴリズムc：課題7b」

http://ynitta.com/class/algoC/local/handin/up.php?id=kadai7b









棒が何本か与えられた時、その棒の中からいくつかを選んで継ぎ足して
(継ぎ足しに必要な長さは0とする)「指定された長さ」ちょうどにする問題を
考えよう。
あなたの仕事は、この問題を解いて何本の棒で「指定された長さ」にできるかを
答えるプログラムを書くことである。
答が何通りかある場合は、そのうちの最小の本数を答えること。
もし、与えられた棒を使って「指定された長さ」ちょうどにできない場合は
-1と答えなさい。




入力形式




入力データは複数のデータセットから成る。
データセットの終わりは2つの 0 で表される。




Dataset1
Dataset2
...
Dataset2
0 0





各データセットは次のような正の整数から成る。




M  N
D1  D2 ... DN





Mは「指定された長さ」である(1≦M≦10000)。
Nは棒の総数(1≦N≦1000)で、
Di は各棒の長さを表す(1≦Di≦1000)。




出力形式




各データセットに対して、答えとなる整数1個を含んだ1行を
出力すること。




サンプル入力
44 10
3 5 7 9 11 13 17 19 23 29
441 10
13 26 38 39 52 65 78 91 104 117
3989 21
19 38 57 76 95 114 133 152 171 190 209 228 247 260 266 285 304 323 342 361 380
0 0






サンプル出力
4
6
-1






dpsum02.txt
3950 30
11 17 29 51 58 68 85 102 119 136 
153 170 187 204 221 238 255 272 289 306 
323 357 374 391 408 425 442 459 476 493
3951 30
11 17 29 51 58 68 85 102 119 136 
153 170 187 204 221 238 255 272 289 306 
323 357 374 391 408 425 442 459 476 493
3952 30
11 17 29 51 58 68 85 102 119 136 
153 170 187 204 221 238 255 272 289 306 
323 357 374 391 408 425 442 459 476 493
1200 33
3 5 7 8 13 15 16 17 19 20 21 23 
25 26 27 30 31 33 35 37 40 41 49 
50 61 64 67 70 71 73 76 77 78
66 33
15 19 23 27 30 33 37 40 41 49 
50 55 61 64 67 70 71 73 76 77 78
83 85 87 88 93 95 97
120 131 135 140 146 
0 0



ヒント1




main()メソッドは次のように書くことができるでしょう。
DPSum.java を自分で作って下さい。
「個数制限ありのナップザック問題」となります。











課題7c









提出ファイルPollock.java


コメント欄:C1_in.txtを入力としたとき、Pollock.javaの出力


提出先:
「宿題提出Web:アルゴリズムc：課題7c」

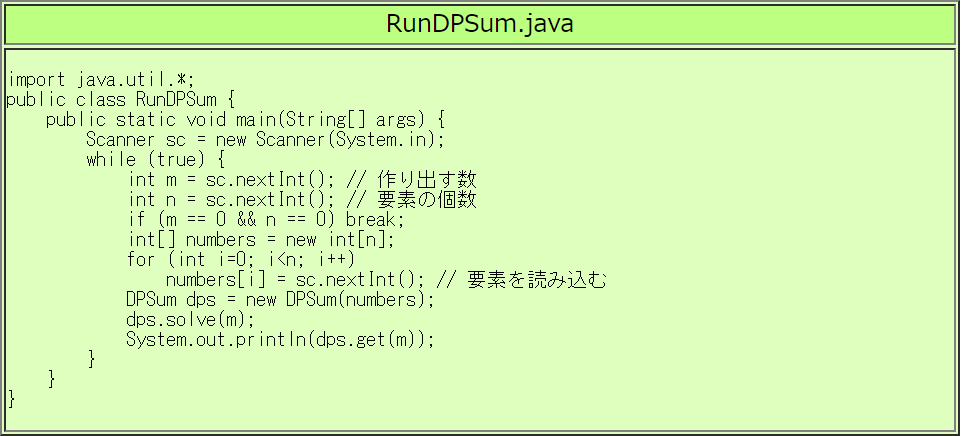
http://ynitta.com/class/algoC/local/handin/up.php?id=kadai7c








「ACM ICPC2010 東京大会予選問題C」より改題。





ポロック予想





n 番目の正三角形数は，最初の n 個の正整数の和と定義される．


n 番目の正四面体数は，最初の n 個の正三角形数の和と定義される．

簡単に示せるように，n 番目の正四面体数は n(n+1)(n+2) ⁄ 6 に等しい．


たとえば，5番目の正四面体数は 1+(1+2)+(1+2+3)+(1+2+3+4)+(1+2+3+4+5)
= 5×6×7 ⁄ 6
= 35 である．







最初の5個の正三角形数


1, 3, 6, 10, 15






Tr[1]Tr[2]Tr[3]Tr[4]Tr[5]






最初の5個の正四面体数


1, 4, 10, 20, 35





Tet[1]Tet[2]Tet[3]Tet[4]Tet[5]







1850年，職業数学者ではなく英国の法律家でありトーリー党（現在の保守党）の政治家でもあった初代准男爵フレデリック・ポロック卿が，すべての正整数は5個以内の正四面体数の和として表現できると予想した．
ただし，和の中で同じ正四面体数が複数回出現してよく，その場合，それぞれの出現を別々に数えるものとする．

この予想は一世紀半以上も未解決なままである．




あなたの任務は，
個別の整数に対してポロック予想が成り立つことを確認するプログラムを書くことである．
あなたのプログラムは，
入力された整数おのおのについて，
それを正四面体数の和として表すための正四面体数の個数の最小値を計算しなくてはならない．





たとえば，40自体は正四面体数ではないが、
40は2個の正四面体数の和
4×5×6 ⁄ 6 + 4×5×6 ⁄ 6
として表すことができる．
したがって，あなたのプログラムに40が与えられると，
2と答えなくてはならない．





Input





入力は行の並びで，
おのおのの行には 106 より小さい正整数がちょうど一つだけ含まれている．

入力の終わりは，一文字の 0 だけを含む行で示される．





Output





入力された正整数おのおのについて，
入力された整数を正四面体数の和として表すために必要な正四面体数の個数の
最小値を含んだ行を出力せよ．
出力に余分な文字が含まれてはならない．





Sample Input




40
14
5
165
120
103
106
139
0



Output for the Sample Input




2
2
2
1
1
5
4
3