 |
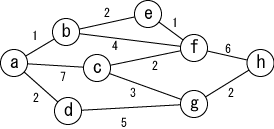
| 図1:グラフの例 |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 表1: 隣接行列 |
「グラフ(graph)」とは「節点(node)」または「頂点(vertex)」を 「辺(edge)」または「枝(branch)」で結んだものです。 グラフの例を図1に示します。 辺の上の数字は、ノード間の距離を表しています。
図1のグラフは表1の隣接行列で表現できます。 ここで、行列の各要素は、ノード間が直接つながっている場合は「距離」に、 つながっていない場合は「-」になっています。 また、同一ノードの間の距離は0であるとしています。
|
|
グラフが与えられた時、始点から終点までの最短距離を求める問題を考えましょう。
前回、学習した「例題:最短経路を求める」という問題は、分岐限定法でそれなりに 高速に解くことができました。 しかし、グラフが複雑になると分岐限定法では非常に時間が掛かってしまいます。 たとえば、 http://ynitta.com/class/algoC/routedata05.txt を先週の RunFindRouteBB.java に与えて動かすと何時間経っても 答は出ません。 都市の数をnとすると、バックトラック法や分岐限定法では基本的に O(n!)の計算時間がかかってしまうからです。
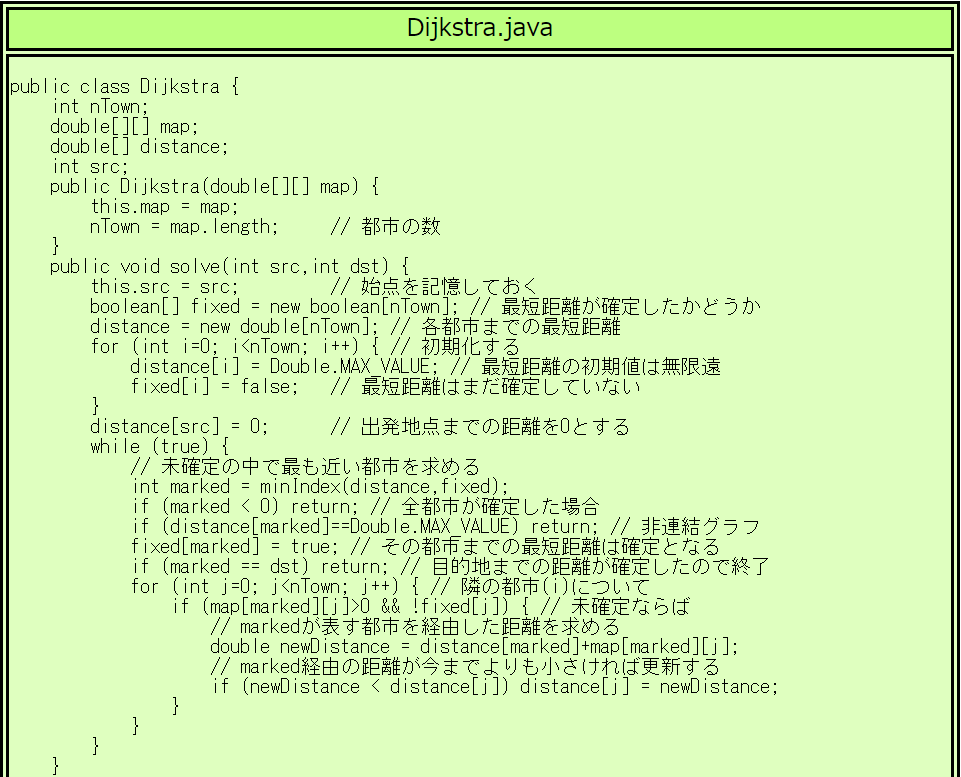
このようなときは「ダイクストラ(Dijkstra)法」を使います。 都市の数をnとすると、ダイクストラ法ではO(n2)で計算できます。
ダイクストラ法とは、各ノードへの最短経路を、始点の周辺から1個所ずつ 確定し、徐々に範囲を広げていく方法です。 グラフにおいてエッジの重みが全て0以上の場合に使うことができます。
 |
出発地点をa、目的地点hとして、最短経路を通った場合の距離を求めましょう。 |
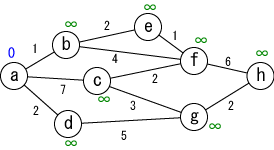 |
全ての地点までの距離を未確定とし、とりあえず無限大としておきます。その上で、出発地点(a)までの距離を0とします。 |
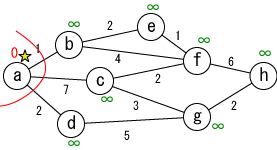 |
未確定の中から距離が最も小さい地点(a)を選んで、その距離を その地点の最小距離として確定します (確定した場所は、赤い曲線で囲んで表しています。 今確定した場所は☆印をつけて表しています。) |
 |
今確定した場所(☆印がついている場所, a)から「直接つながっている」 かつ「未確定の」地点(b,c,d)に関して、今確定した場所(a)を経由した場合の距離を 計算し、今までの距離よりも小さければ書き直します。 (b,c,dがそれぞれ∞から1,7,2に書き替りました)。 |
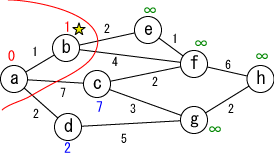 |
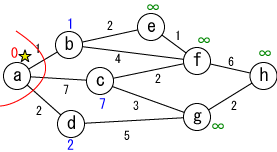
未確定の中から距離が最も小さい地点(b)を選んで、その距離を その地点の最小距離として確定します。 もし、最小値を持つ地点が複数ある場合は、そのなかのどれを 選んでも構いません。 今確定した場所(b)を☆印をつけて表しています。 |
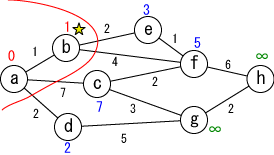 |
今確定した場所(☆印がついている場所, b)から「直接つながっている」 かつ「未確定の」地点(e,f)に関して、今確定した場所(b)を経由した場合の距離を 計算し、今までの距離よりも小さければ書き直します。 (e,fがそれぞれ3,5に書き替りました)。 |
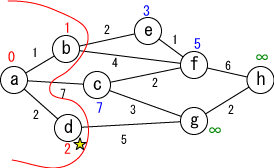 |
未確定の中から距離が最も小さい地点(d)を選んで、その距離を その地点の最小距離として確定します。 |
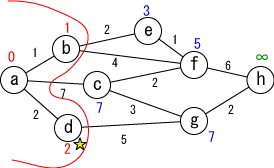 |
今確定した場所(☆印がついている場所, d)から「直接つながっている」 かつ「未確定の」地点(g)に関して、今確定した場所を経由した場合の距離を計算し、 今までの距離よりも小さければ書き直します。 (gが7に書き替りました)。 |
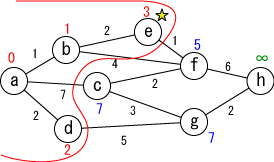 |
未確定の中から距離が最も小さい地点(e)を選んで、その距離を その地点の最小距離として確定します。 |
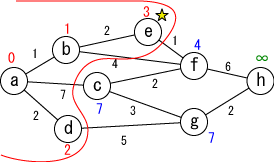 |
今確定した場所(☆印がついている場所, e)から「直接つながっている」 かつ「未確定の」地点(f)に関して、今確定した場所を経由した場合の距離を計算し、 今までの距離よりも小さければ書き直します。 (fが4に書き替りました)。 |
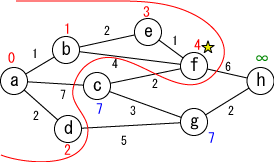 |
未確定の中から距離が最も小さい地点(f)を選んで、その距離を その地点の最小距離として確定します。 |
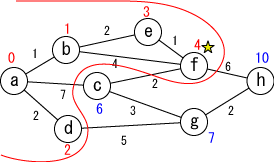 |
今確定した場所(☆印がついている場所, f)から「直接つながっている」 かつ「未確定の」地点(c,h)に関して、今確定した場所を経由した場合の距離を計算し、 今までの距離よりも小さければ書き直します。 (c,hがそれぞれ6,10に書き替りました)。 |
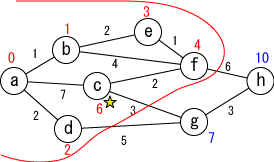 |
未確定の中から距離が最も小さい地点(c)を選んで、その距離を その地点の最小距離として確定します。 |
 |
今確定した場所(☆印がついている場所, c)から「直接つながっている」 かつ「未確定の」地点(g)に関して、今確定した場所を経由した場合の距離を計算し、 今までの距離よりも小さければ書き直します。 (gは書き替りませんでした)。 |
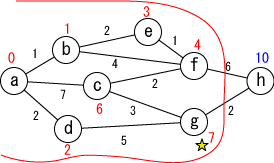 |
未確定の中から距離が最も小さい地点(g)を選んで、その距離を その地点の最小距離として確定します。 |
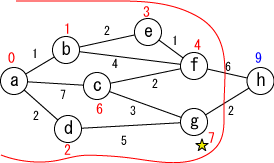 |
今確定した場所(☆印がついている場所, g)から「直接つながっている」 かつ「未確定の」地点(h)に関して、今確定した場所を経由した場合の距離を計算し、 今までの距離よりも小さければ書き直します。 (hは9に書き替りました)。 |
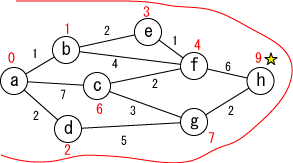 |
未確定の中から距離が最も小さい地点(h)を選んで、その距離を その地点の最小距離として確定します。 これで全ての地点までの最短距離が確定しました。 |
いくつかの都市と、それらの都市をつなぐ道路の距離が与えられている。 出発地点と目的地点が与えられたとき、最短経路を探すプログラムを 作りなさい。
入力
N R A1 B1 L1 A2 B2 L2 ... AR BR LR S D
最初の行には2個の整数 N と R が含まれる。 N は都市の数(ただし1≦N≦100)を表し、 Rはそれらの都市をつなぐ道の個数を表す。 2行目以降はR行に渡って、3個の整数 Ai, Bi, Li が含まれる(1≦i≦R)。 Ai と Biは道の両端の都市を表し (0≦Ai≦N-1, 0≦Bi≦N-1)、 Liは道の距離を表す(1≦Si≦1000)。 その次の行に2個の整数 S, D が含まれる。 S は出発地点の都市を表し、Dは目的地点の都市を表す (0≦S≦N-1, 0≦D≦N-1)。
出力
答が発見された場合は、最初の行に「最短経路の距離」を表す整数を出力し、 次の行に「 最短経路を辿ったときの都市を、出発地点から 目的地点まで順にスペースを1個ずつあけて」出力しなさい。 最短経路が複数ある場合は、そのうちの1つの経路を答えとすればよい ものとする。 答が無い場合は、"No route"と出力しなさい。
ここではダイクストラ法をjavaであえて愚直にプログラミングした例を示します。 このプログラムでも先週の分岐限定法よりは随分高速化されていることがわかります。 愚直ではないプログラミング例は次回の授業で示します。 (どのような工夫でどれだけ高速化されるかを段階を経て理解してもらうのがねらいです)。

| RunDijkstra.javaの実行例 |
% javac RunDijkstra.java Dijkstra.java % java RunDijkstra < routedata05.txt 70.0 |
最短経路を表示するように変更してみましょう。
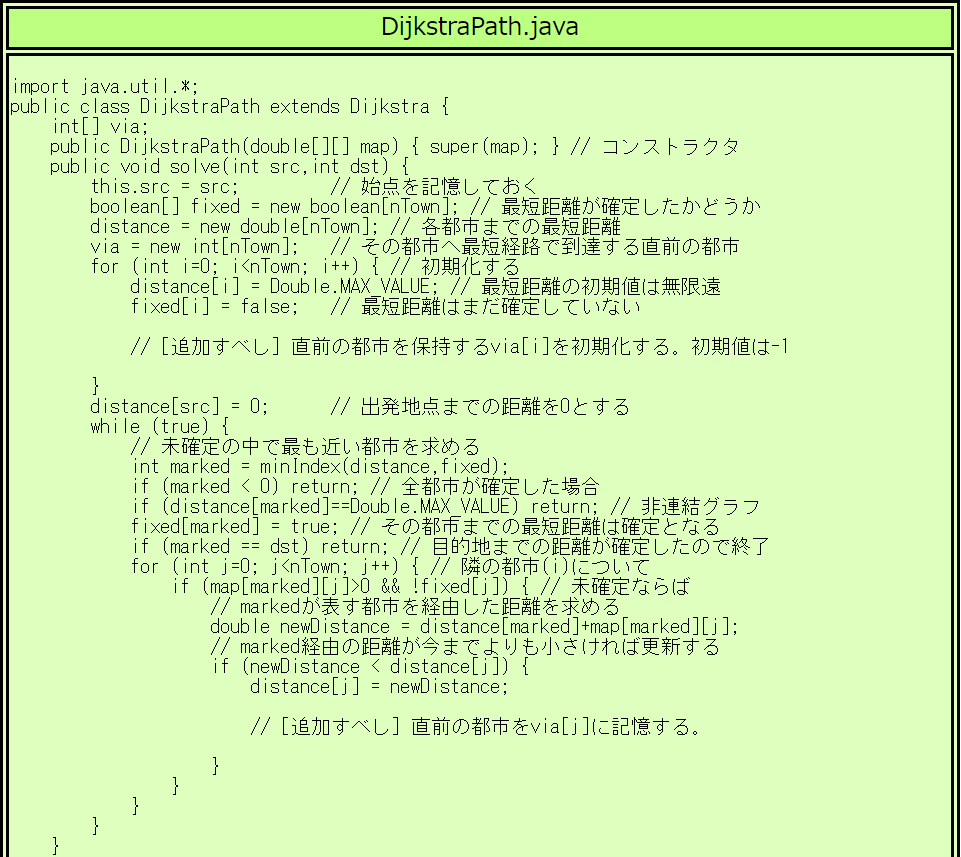
各地点の距離を更新するときに、どの地点を直前に経由したのかを 記録するようにします。
下の DijkstraPath.java では、都市 i に到達する直前の都市を via[i] に記憶するようにしています。 プログラム中には2行だけ欠けている部分がありますので、自分で考えて その2行を追加して下さい。


| RunDijkstraPath.javaの実行例 |
% javac RunDijkstraPath.java DijkstraPath.java Dijkstra.java % java RunDijkstraPath <routedata05.txt 70.0 [0 150 200 240 332 229 300 400 557 466 500 600 764 786 700 800] |
ダイクストラ法では、 n個のノード全てについて最短距離を確定するために近い順に最短距離を 確定させていきます(n回の繰り返しが必要)。 その繰り返しの中で毎回「まだ最短距離が確定していないノードの集合から 最小距離のノードを選択し、選択した要素とつながっているノードの 距離を更新する」という操作をします (nに比例する数の要素を調べる必要)。 したがって、O(n×n)=O(n2)の計算量が必要であることがわかります。
計算量のオーダーは変わりませんが、疎なグラフ(つまりノード間に あまりエッジがないグラフ)では、ノード間の接続関係を隣接行列で 表現するよりも隣接リストで表現するべきです。
| 注意 |
|
routedata10.txtを入力として RunDijkstra.javaを実行する場合は、 java のヒープの大きさを広げて下さい。 実行環境によっても異なりますが、津田塾大学のMac上の環境では 600M Byte以上にすればヒープが不足することは無いようです。 たとえばヒープを1400M byteで実行するには以下のように指定します。 time (java -Xmx1400M RunDijkstra < routedata10.txt) また、プログラムの実行時間の表示に関してですが、 Mac上のtimeコマンドでは次のような表示となります。 real 0m2.167s ←この値を採用して下さい user 0m3.293s system 0m0.528sこのように3種類の値が表示されるはずですが、realとして表示されている 値を採用して下さい。mは分、sは秒を表していますので、上の例では 2.167秒ということになります。 |
作成したプログラムが正しく動作することを確認したら、それぞれの 提出先に提出しなさい。
提出した後は、正しく提出されていることを http://ynitta.com/class/algoC/local/handin/ で必ず確認しておいて下さい。
課題提出〆切は次回の講義の開始時刻です。
| 提出ファイル | DijkstraPath.java |
|---|---|
| コメント欄: | routedata04.txtを入力としたとき、RunDijkstraPath.javaの出力 |
| 提出先: | 「宿題提出Web:アルゴリズムc:課題3a」 http://ynitta.com/class/algoC/local/handin/up.php?id=kadai3a |
RunDijkstraPath.javaを http://ynitta.com/class/algoC/routedata04.txt に対して動作させて下さい。
| 提出ファイル | Dijkstra.java |
|---|---|
| コメント欄: | routedata10.txtを入力としたとき、RunDijkstra.javaの実行時間 |
| 提出先: | 「宿題提出Web:アルゴリズムc:課題3b」 http://ynitta.com/class/algoC/local/handin/up.php?id=kadai3b |
RunDijkstra.javaを http://ynitta.com/class/algoC/routedata10.txt に対して動作させて time コマンドで時間を測って下さい。
実行時にヒープ領域を広げないと「メモリが足りない」という 例外が起きて計算が途中で終了してしまうので、実行時間が 正しく計測できないかもしれないので注意して下さい。