|
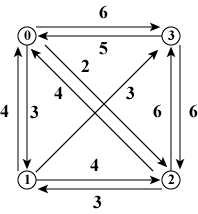
| 図1: グラフ |

|
|
|
|
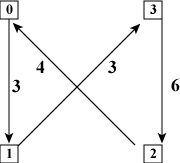
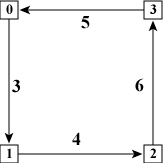
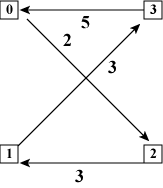
| (a) 0-3-2-1-0 | (b) 0-1-3-2-0 | (c) 0-1-2-3-0 | (d) 0-2-1-3-0 |
| 図2: 全てのノードを訪れた後スタートに戻る経路 | |||
巡回セールスマン問題(じゅんかいセールスマンもんだい、英: travelling salesman problem、TSP)は、都市の集合と各2都市間の移動コスト(たとえば距離)が与えられたとき、全ての都市をちょうど一度ずつ巡り出発地に戻る巡回路の総移動コストが最小のものを求める(セールスマンが所定の複数の都市を1回だけ巡回する場合の最短経路を求める)組合せ最適化問題である。
問題例の大きさは、都市の数で表される。この問題は、計算複雑性理論においてNP困難と呼ばれる問題のクラスに属する。すなわち、問題例の大きさに関する決定性の多項式時間アルゴリズムが見つかりそうにない、計算量的に困難な問題である。なお、この問題の特殊ケースとして考えられるハミルトン閉路問題は、NP困難であると共にNP完全と呼ばれるクラスにも属するので、扱いが異なる。
単純に考えると O(n!) の計算量が必要ですが、 DP (Dynamic Programming)を使うと O(2n n2)の計算量で 解くことができます。
巡回セールスマン問題の例として、 4個のノードが有向エッジで連結された図1のグラフを考えましょう。 ノード0からスタートして、全てのノードを経由してノード0に戻ってくる 経路は、図2(a)〜(d)に示すように4通りあります。 図では「まだ訪れていないノード」を「丸」で、 「既に訪れたノード」を「四角」で表しています。
|
| ||||||||||||||
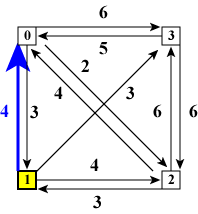
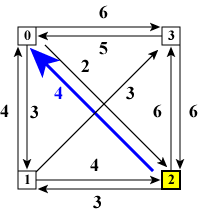
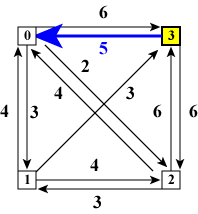
さて、図2の「ノード0をスタートしてから全てのノードを訪れた後ノード0に戻る経路」 ですが、スタートノードに戻る直前のノード(= last )が 「ノード1である」場合(図3(a)), 「ノード2である」場合(図3(b)), 「ノード3である」場合(図3(c))の3通りあります。 図3では、最後に訪れたノードを黄色い四角で表現しています。 循環経路のコストは 「ノード0をスタートしてからノードlastまでのコスト」+ 「ノードlast からノード0へのエッジのコスト」 で計算できます。
|
|
| |
| (a)ノード1から戻る | (b)ノード2から戻る | (c)ノード3から戻る | |
| 図3:全ノードを訪れた後 | |||
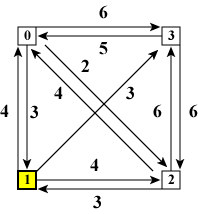
図3(c)は図2(c)と図2(d)の両方の場合に相当していることに注意して下さい。 すなわち、「既に訪れたノード群」と「最後に訪れたノード」に基づいて 状態を区別し、「最後に訪れたノード以外のノードの順番は気にしない」 ことにします。
|

|

| |
| (a)ノード1が最後 | (b)ノード2が最後 | (c)ノード3が最後 | |
| 図4:全ノードを訪れた時 | |||
図4の3種類の状態のうち、例として、 図4(a)の 「全ノードを訪れたときノード1が最後」を詳しく見ていくことにしましょう。 この状態を実現するためには「ノード0,2,3を訪れた状態」からノード1に 移動する必要があります。 図5では、 強調のため既に訪れたノード群を赤線で囲んでいます。
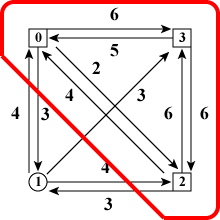 |
| 図5: 図4(a)のひとつ前の状態 |
図5の状態は、既に訪れたノード0,2,3,のうちどのノードを最後に訪れたかで
3種類あります(図6)。
図4(a)に至るコストは、x を0,2,3のどれかとして、
「ノード0,2,3を全て訪れた状態で、最後に訪れたノードがx のコスト」
+「ノードx とノード1を結ぶエッジのコスト cx1」
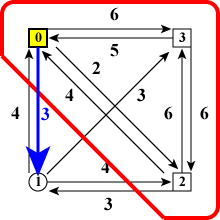
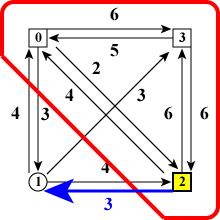
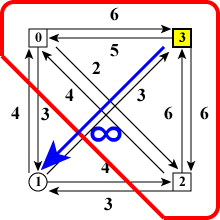
であることがわかります。すなわち、図6(a)〜(c)の
「赤線で囲まれた状態に至る最小コスト」+「青い太矢印のコスト」
を計算して、それらの中から最小値を選べば図4(a)に至る最小コストがわかります。
図6(c)では、ノード3からノード1に向かうエッジが存在しないのでコスト c31 は無限大となっています。
ノード0はスタートノードですから、ノード0, 2, 3 を回った状態で ノード0からノード1にくることは実際にはありえないのですが、 ここでは説明やプログラムを簡単にするためスタートノードも 入れて考えておきます。
|
|
|
| (a)ノード0が最後 | (b)ノード2が最後 | (c)ノード3が最後 |
| 図6:ノード0,2,3を訪れた時 | ||
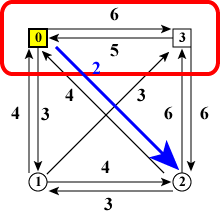
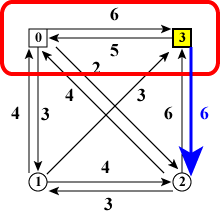
図6の3種類のうち、例として、 図6(b)「ノード0,2,3を訪れたときノード2が最後」の状態を詳しく見ていきましょう。 この状態を実現するためには「ノード0,3を訪れた状態」からノード2に移動する 必要があります(図7, 強調のため既に訪れたノード群を赤線で囲んでいます)。
 |
| 図7: 図6(b)のひとつ前の状態 |
図6(b)に至るコストは、x を0,3のどれかとして、
「ノード0,3を全て訪れた状態で、最後に訪れたノードがx のコスト」
+「ノードx とノード2を結ぶエッジのコスト cx2」
です。
それらの中から最小値を選べば、図6(b)に至る最小コストがわかります。
|
|
| (a)ノード0が最後 | (b)ノード3が最後 |
| 図8:ノード0,3を訪れた時 | |
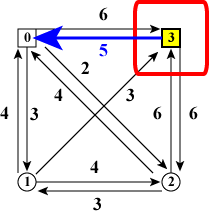
図8(a)の状態になるには、図9のように 「ノード3だけを訪れている状態」からノード0に移動する 必要があります。 しかし、これはすなわち図11(d)の「ノード3からスタートする」 という状態なので条件を満たしません。 不可能な状態のコストは無限大と考えます。
図8(b)の状態になるには、図10のように 「ノード0だけを訪れている状態」からノード3に移動する必要があります。 これは図11(a)のスタート地点にいる状態ですからコストは0です。
 |
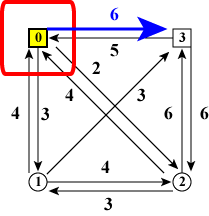 |
| 図9: 図8(a)のひとつ前の状態 | 図10: 図8(b)のひとつ前の状態 |
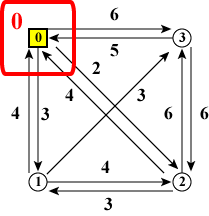
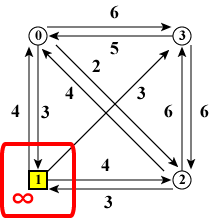
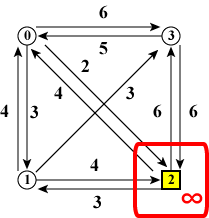
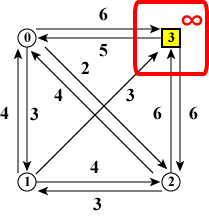
1個のノードだけを訪れている状態が初期状態であり、ノードの個数だけ存在します。 「スタートノードに最初にいる状態」のコストは 0 ですが、 スタートノード以外に最初にいる状態は不適切で解には成り得ないので コストは無限大としておきます。
|
|
|
|
| (a)ノード0 | (b)ノード1 | (c)ノード2 | (d)ノード3 |
| 図11:スタート地点とコスト | |||
以上で説明してきたように、巡回セールスマン問題をDPで解くには、 「あるノードの集合Sを全て訪れていて、最後に訪れたノードがx である (x ∈ S)」 状態に至る最小コストを計算するために、 「集合Sからx を除いた集合S' について、 S'は全て訪れていて最後に訪れたノードがy である(y ∈ S')」状態に至る最小コスト +「y からx に向かうエッジのコスト cyx」を使います。 ノードを減らしていくと、最後にはノードがひとつ残るので そこがスタート地点になるわけです。
下に示すプログラム例では、巡回の途中でyの候補として スタートノードも選んでいますので、余分な計算をしています。 訪れたノード群が2個以上の場合はスタートノードは候補に入れない、 訪れたノード群が1個の場合はスタートノードで決め打ちをする、 というプログラムにした方がよいでしょう。
全体を説明した図はこちら
図1のグラフにおける巡回セールスマン問題をDPで解くための表について説明します。
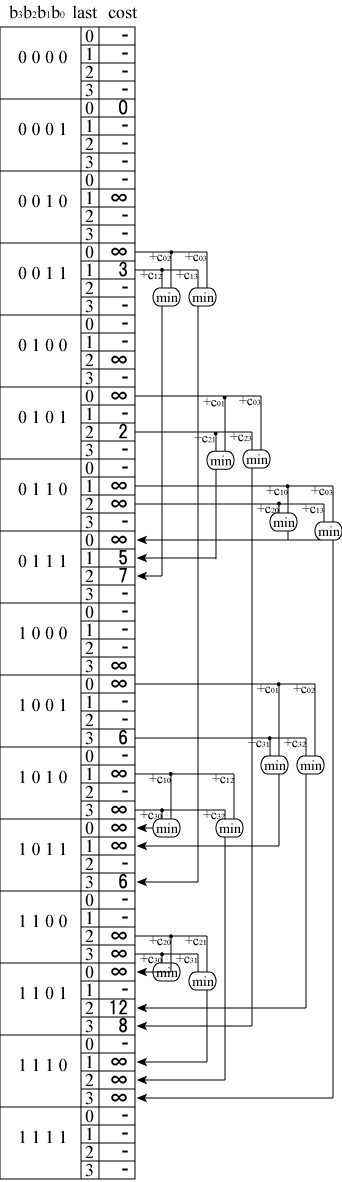
既に訪れたノード群をn bit幅のビットパターンで表現することにします。 すなわち、 bn-1 ... b2 b1 b0 において「右からi 番目のビット bi の値が、 ノードi を訪れたかどうかを表す(訪れれば1,訪れていなければ0) ものとします。 また、最後に訪れたノードをlastとして、整数で保持します。 このbn-1 ... b2 b1 b0と last の組を bn-1 ... b2 b1 b0:last と表記することにします。
bn ... b2 b1 b0:last を表のインデックスとして、表にはその状態に至る最小コストを記録します。 したがって、必要なメモリ量は O(2n n)となります。
初期状態では、 スタート地点である0001:0のコストを0に, 0010:1, 0100:2, 1000:3 を無限大に、 他は全てUNKNOWN(図ではマイナス記号)としておきます(図12(a))。
ノードを1個だけ訪れた状態を使って、ノードを2個訪れた状態に至る 最小コストを計算します(図12(b))。
ノードを2つだけ訪れた状態を使って、ノードを3つ訪れた各状態に至る最小コストが 計算できます(図12(c))。
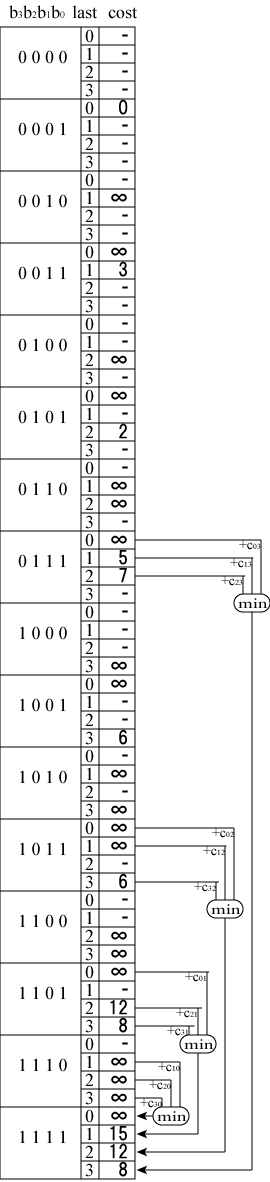
ノードを3つだけ訪れた状態を使って、ノードを全て(4つ)訪れた各状態に至る 最小コストが計算できます(図12(d))。 図12(d)の中の、ノードを全て訪れた状態である 1111:1, 1111:2, 1111:3 のコストに、エッジのコスト c10, c20, c30 をそれぞれ加えた中から最小値を探せば答となります。
 |
 |
 |
 |
 |
| (a)初期状態(1個) | (b)2個 | (c)3個 | (d)4個 | (e)スタートへ戻る |
| 図12: 訪れたノードがk-1個の状態から、k個の状態の最小コストを求める | ||||
N M S F1 T1 C1 ... FM TM CM
Nは2以上の自然数でノードの総数を表す。 ノード番号は0, 1, ..., N-1となる。 Mは自然数で有向エッジの総数を表す。 SはN未満の自然数で、スタートするノードを表す。 Fi Ti Ci は、ノードFiからノードTiに向けて 有向エッジが存在しそのコストは Ci であることを表す。 FiとTiは0以上N-1以下の整数で、 Ciは0以上の実数である。 あるノードのペアに対して、一方からもう一方へ向かう 向かうエッジの本数は高々1本である。
| ts4_data.txt |
4 11 0 0 1 3.0 1 0 4.0 0 2 2.0 2 0 4.0 0 3 6.0 3 0 5.0 1 2 4.0 2 1 3.0 1 3 3.0 2 3 6.0 3 2 6.0 |
指定されたノードをスタートして、 全てのノードを重複せずに訪れた後、 スタートノードに戻った場合の最小コストを実数値として出力せよ。 不可能の場合は -1 と出力すること。
javaのコードを示します。 コストを実数とすると、記録用のメモリは実数の2次元配列で表現できます (1次元配列でも表現可能ですが、ここでは簡単のために2次元配列を使っています)。
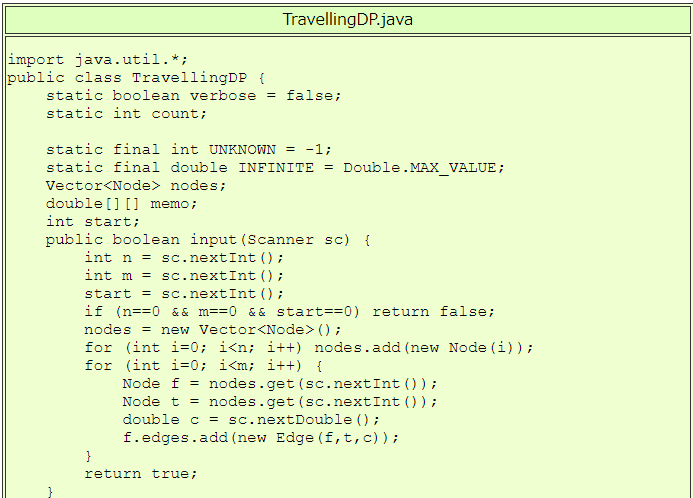
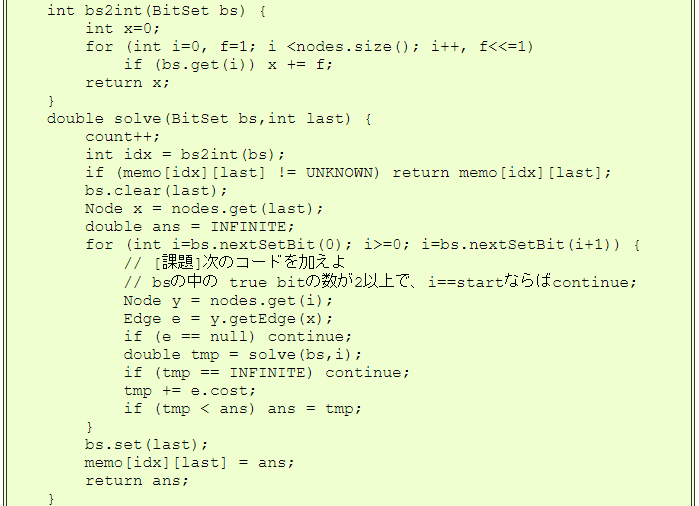
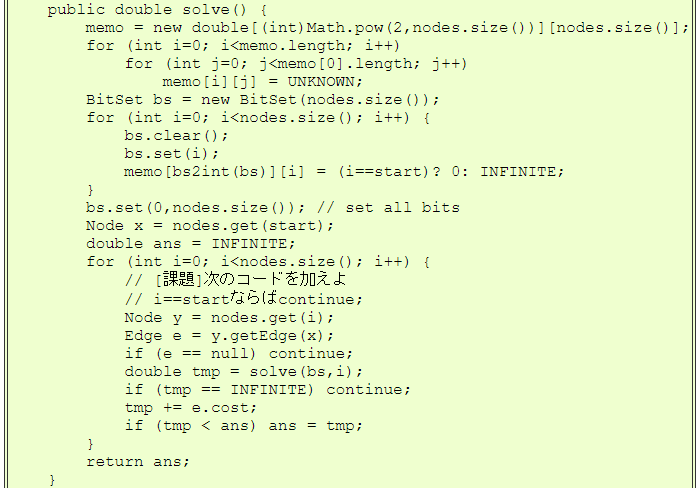
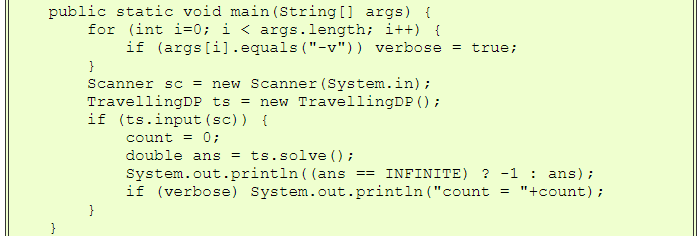

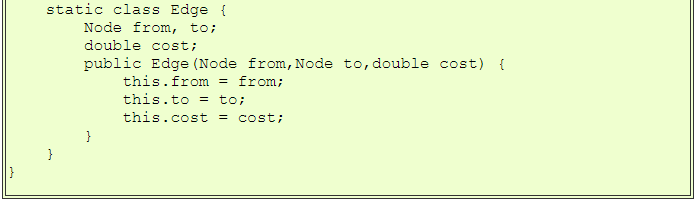
| TravellingDP.javaの実行例 |
$ javac TravellingDP.java $ java TravellingDP < ts4_data.txt 13.0 $ java TravellingDP -v < ts4_data.txt 13.0 count = 15 |
作成したプログラムが正しく動作することを確認したら、それぞれの 提出先に提出しなさい。
提出した後は、正しく提出されていることを http://ynitta.com/class/algoC/local/handin/ で必ず確認しておいて下さい。
〆切は次週の金曜日13:00です。
| 提出ファイル | TravellingDP.java |
|---|---|
| コメント欄: | 変更後のプログラムで、ts10_data.txt, ts16_data.txt, ts18_data.txt を処理したとき、double solve(BitSet,int) メソッドの 呼び出し回数がそれぞれ何回になるか答えなさい。 |
| 提出先: | 「宿題提出Web:アルゴリズムc:課題10a」 http://ynitta.com/class/algoC/local/handin/up.php?id=kadai10a |
上記のプログラムで次のデータ
を処理した結果は以下の通りです。| TravellingDP.javaの実行例 |
$ java TravellingDP -v <ts10_data.txt 39.0 count = 【課題: この数字を答えよ】 $ java TravellingDP -v < ts16_data.txt 40.0 count = 【課題: この数字を答えよ】 $ java TravellingDP -v < ts18_data.txt 42.0 count = 【課題: この数字を答えよ】 |
プログラム中の注釈で示してある変更を加えなさい。 変更後のプログラムで、ts10_data.txt, ts16_data.txt, ts18_data.txt を処理したとき、double solve(BitSet,int) メソッドの 呼び出し回数 (= -vオプションをつけて実行したときのcountの値) がそれぞれ何回になるか答えなさい。
この課題はoptional です。できた人だけが提出して下さい。
| 提出ファイル | ICPC2011F.java |
|---|---|
| コメント欄: | 正解判定用の入力データを正しく処理して 正解判定用の出力データを出力するのに かかった秒数。 |
| 提出先: | 「宿題提出Web:アルゴリズムc:課題10b」 http://ynitta.com/class/algoC/local/handin/up.php?id=kadai10b |
ACM ICPC 2011 Asia Regional Contest, Fukuoka の F問題を解け。 ただし、正解判定用データの処理時間が30秒以下のプログラムのみ正解とする。
複数の都市が合併することになったので、新しい都市の名前を考えることになった。 ただし、「新しい都市の名前には元の各都市の名前が入っているべきだ」という 意見が通ってしまった。 新しい都市の名前はなるべく短くしたい(= alphabet数を減らしたい)ので、 単にconcatenateするだけでは長くなりすぎる。
あなたの使命は、都市名がいくつか与えられたとき 元の都市の名前を全て含んだ最も短い文字列を探す プログラムを書くことである。 たとえば、 FUKUOKA, OKAYAMA, YAMAGUCHIという3都市の名前が与えられた場合は FUKUOKAYAMAGUCHI が答である。 ただし、この文字列は FUKUYAMA という都市名も元の文字の順番と同じに 含んでいるが、文字が連続していないのでFUKUYAMAは含んでいるとは見なさない。
入力は複数のデータセットからなる。各データセットは最初の行は 自然数n (n ≤ 14) であり、これは都市の名前の個数を表す。 続く n 行に、各行に一つずつ都市名が並ぶ。 都市名は、20文字以下の大文字のアルファベットである。 ひとつのデータセットの中に同じ名前の都市は表れない。
入力の終わりは0だけを含んだ行で表現する。
各データセットに対し、整数を1個含んだ行を出力せよ。 整数は、新しい都市名として可能な文字列のうち最短文字数である。
| サンプル入力 |
3 FUKUOKA OKAYAMA YAMAGUCHI 3 FUKUOKA FUKUYAMA OKAYAMA 2 ABCDE EDCBA 4 GA DEFG CDDE ABCD 2 ABCDE C 14 AAAAA BBBBB CCCCC DDDDD EEEEE FFFFF GGGGG HHHHH IIIII JJJJJ KKKKK LLLLL MMMMM NNNNN 0 |
| サンプル出力 |
16 19 9 9 5 70 |
巡回セールスマンと同様に O(2n n2)のアルゴリズムで 解くことができます。
巡回セールスマン問題と、ICPC2011 問題Fの違いは以下の通りです。
どのノードからスタートしてもよいこと、 スタートしたノードに戻る必要がないことから、 次のようなコードで書くことができます(が、もちろん、自分で0から 書いたプログラムを提出しても構いません)。
| NittaF.java |
import java.util.*;
public class NittaF {
static final int UNKNOWN = -1;
static final int INFINITE = Integer.MAX_VALUE;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
Solver sol = new Solver();
while (sol.input(sc)) System.out.println(sol.solve());
}
static class Solver {
int[][] tbl;
int[][] memo;
ArrayList<String> v;
public boolean input(Scanner sc) {
v = new ArrayList<String>();
ArrayList<String> omit = new ArrayList<String>();
int n = sc.nextInt();
if (n==0) return false;
for (int i=0; i<n; i++) {
String s = sc.next();
boolean flag=true;
for (String x: v) {
if (x.contains(s)) flag=false;
else if (s.contains(x)) omit.add(x);
}
if (flag) v.add(s);
}
for (String s: omit) v.remove(s);
return true;
}
public static int nMatches(String p,String q) {
int k=0;
for (int i=1; i<=p.length()&&i<=q.length(); i++)
if (p.regionMatches(p.length()-i,q,0,i)) k=i;
return k;
}
int bs2int(BitSet bs) {
int x=0;
for (int i=0,f=1; i<v.size(); i++,f<<=1)
if (bs.get(i)) x += f;
return x;
}
public int solve(BitSet bs,int last) {
// [課題] 正しく動作するコードを書きなさい
// memo[bsが表す整数値][last] がUNKNOWNでなければその値を返す
// bsの第last bitをclearして
// bsの中の各set bitについて繰り返し(第iビットとする)
// bsのset bit中で第i番目の文字列が最後の場合の最小文字数
// +第i番目の後ろに第last番目の文字列を付加して増える文字数
// の最小値を求める
// memo[bsが表す整数値][last] にその最小値を入れる
// bsを元に戻して (第last bitをsetし直して)
// 最小値を返す
}
public int solve() {
tbl = new int[v.size()][v.size()];
for (int i=0; i<v.size(); i++)
for (int j=0; j<v.size(); j++)
tbl[i][j] = nMatches(v.get(i),v.get(j));
memo = new int[(int)Math.pow(2,v.size())][v.size()];
for (int i=0; i<memo.length; i++)
for (int j=0; j<memo[i].length; j++)
memo[i][j] = UNKNOWN;
BitSet bs = new BitSet(v.size());
for (int i=0; i<v.size(); i++) {
bs.clear();
bs.set(i);
memo[bs2int(bs)][i] = v.get(i).length();
}
bs.set(0,v.size());
int ans=INFINITE;
for (int i=0; i<v.size(); i++) {
int ret = solve(bs,i);
if (ret<ans) ans=ret;
}
return ans;
}
}
}
|