今まで見てきた「キーの大小を比較して整列」するアルゴリズムは 計算量の下限が $O(n \log n )$ になることが理論的に 証明されています。
ところが、キーの大小を比較しない方法を使うと $O(n)$ の計算時間で整列が可能です。 ただし、キーがある条件を満していなければなりませんが。
「キーが整数で、ある範囲に収まっていて、重複がない」場合に ビンソートが使えます。 キーの取り得る値全てについてデータの記憶場所(bin、ビン)を確保し、 キーにしたがってデータをビンに入れていきます。 最後に、ビンを前から順に集めれば、昇べきの順でデータを整列したことになります。 (p.381, Fig.17.1)
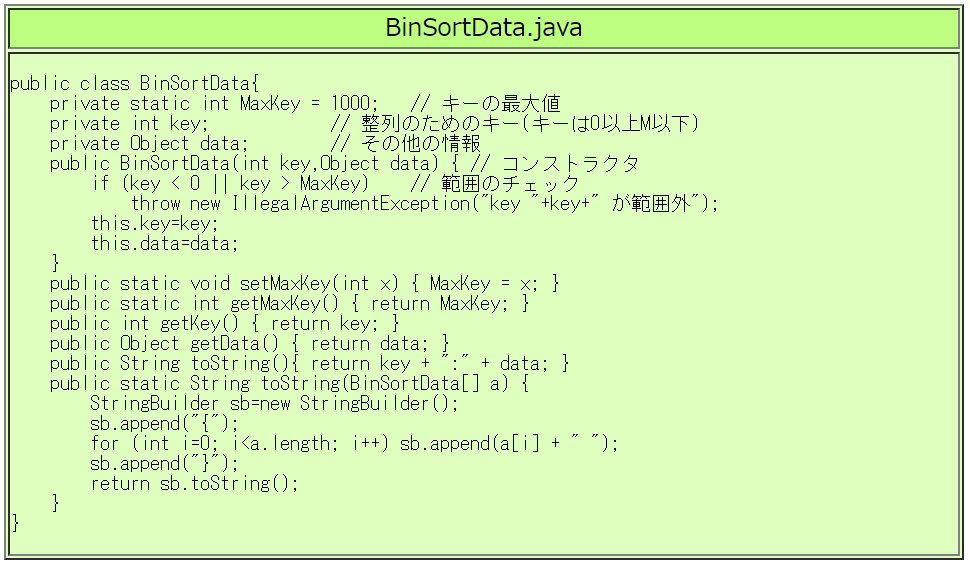
| RunBinSort.javaの実行例 |
|
データの個数を $n$ , 用意したビンの個数を$m$ とすると、
$n$ 個のデータをビンに振り分ける手間は $O(n)$となるので、これらを合計して、
データをビンから取り出す手間は $O(m)$
ビンソートの計算量は $O(n+m)$となります。$m$ が $n$ に比べて極端に大きくなければ $m$ は $n$ と同程度(少なくとも定数倍)とみなされるので
ビンソートの計算量は $O(n)$となります。
ビンソートにおける「重複したデータがない」という条件を緩めて、 「重複したデータがあっても構わない」としたソートが 「分布数え上げソート」です。
p.390 Table17.1 データ: 7, 1, 4, 2, 7, 8, 2
| キー k | 出現回数 a | 累計 b |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 2 | 3 |
| 3 | 0 | 3 |
| 4 | 1 | 4 |
| 5 | 0 | 4 |
| 6 | 0 | 4 |
| 7 | 2 | 6 |
| 8 | 1 | 7 |
| 9 | 0 | 7 |
| 10 | 0 | 7 |
累計[i]は、キーが0〜iの間にあるデータの個数となります。 データの置き場所として、0番目から数えているので、 キーが i のデータは (累計[i-1])番目 または(累計[i] - 1)番目に 配置すればよいわけです。
教科書では、キーが0の場合でも特別扱いが必要ない 「(累計[i] - 1)番目に配置する」方式をとっています。
データを配置する度に 「累計[i] = 累計[i] - 1」とすれば キーの値が同じ複数のデータがあってもうまく配置できます。 ただし、この場合、キーの値が同じデータは「後ろから前へ」と 並べられることになりますので、 ソートしたデータが「安定である(＝同じキーの値を持つデータ同士では、 元の順序関係がソート後の順序でも保持される)」ためには、 元のデータが後にあったものから配置する必要があります。
| RunDistributionCountingSort.javaの実行例 |
|
データの個数をn, 分布表の要素数をmとすると、
分布表を用意する $O(m)$となり、全体の計算量は $O(n+m)$ となります。 $m$ が $$ nに比べて極端に大きくなければ(定数倍程度ならば)、 計算量は $O(n)$ とみなせます。 もし $m$ が $n$ に比べて極端に大きければ $O(m)$ とみなせます。
データのキーの分布を調べる $O(n)$
キーの累積度数分布を求める $O(m)$
度数分布にしたがってデータを配置する $O(n)$
(ソートしたデータを元の配列に書き戻す $O(n)$ )
作成したプログラムが正しく動作することを確認したら、それぞれの 提出先に提出しなさい。
提出した後は、正しく提出されていることを http://ynitta.com/class/algoB/local/handin/ で必ず確認しておいて下さい。
課題提出〆切は次回の講義開始時刻です。
| 提出ファイル | BinSort.java |
|---|---|
| コメント欄: | RunBinSort.javaに例と同じデータを与えた時の出力 |
| 提出先: | 「宿題提出Web:アルゴリズムB：課題7a」 http://ynitta.com/class/algoB/local/handin/up.php?id=kadai7a |
上記の BinSortData.java, BinSort.java, RunBinSort.java を自分で入力し、 動作させてみましょう。 動作を確実に理解して下さい。
| 提出ファイル | RunDistributionCountingSort2.java |
|---|---|
| コメント欄: | 分布数え上げソートがrand800k.txt, inc800k.txt, dec800k.txtをそれぞれソートするのにかかる時間 |
| 提出先: | 「宿題提出Web:アルゴリズムB：課題7b」 http://ynitta.com/class/algoB/local/handin/up.php?id=kadai7b |
課題2で使った http://nw.tsuda.ac.jp/class/algoB/sortdata/の下の 3種類のデータ
RunDistributionCountingSort.java を参考にして、 標準入力から上記のデータを読み込んでソートする RunDistributionCountingSort2.javaを作りなさい。
さらに、DistributionCountingSort2.javaが、rand800k.txt, inc800k.txt, dec800k.txtを読み込んでソートするのに必要な時間を それぞれ計測し、答えなさい。 結果の出力にかかる時間を含めたくないので、実行時間を計測する場合は ソートし終わった状態を標準出力に表示するコードをコメントアウトしてから 測るのが望ましい。
[注意] DistributionCountingSortクラスは BinSortDataオブジェクトの 配列をソートしますが、今回扱うデータは整数値のみです。 そこで、データをkeyフィールドに保存し、dataフィールドには keyと同じ値のIntegerオブジェクトを入れておけばよいものとします。
| 提出ファイル | RunBinSort2.java |
|---|---|
| コメント欄: | (最小のデータを $0$ 番目と表現する数え方で)小さい方から $5$ 番目と $10$ 番目のデータ 入力ファイルは次の2種類。 http://ynitta.com/class/algoB/bindata01.txt http://ynitta.com/class/algoB/bindata02.txt |
| 提出先: | 「宿題提出Web:アルゴリズムB：課題7c」 http://ynitta.com/class/algoB/local/handin/up.php?id=kadai7c |
複数の整数値がデータとして与えられる。 データに重複した値を持つものはなく、さらにデータの最小値と 最大値の差は $100000$ 以下であるものとする。
BinSort.javaを用いて、入力されたデータを小さい順に並べ替えて 指定された順番のデータを表示するRunBinSort2.javaを作成しなさい。
入力データ形式は次の通り。
$N$
$D_1$
$D_2$
$\cdots$
$D_N$
$N$ はデータの個数である。 $D_i$ はデータで整数値である。
$11 \leqq N \leqq 100000$
$-1000000000 \leqq D_i \leqq 1000000000$
$0 \leqq \max(D_i) - \min(D_i) \leqq 100000$
| RunBinSort2.javaの実行例 |
|
[注意] BinSortクラスは BinSortDataオブジェクトの配列をソートしますが、 課題7a, 7b では扱うデータは整数値のみです。 そのような場合は、データをkeyフィールドに保存し、dataフィールドにはkeyと同じ値の Integerオブジェクトを入れておけばよいものとします。 課題7cではデータから最小値を引いたものをキーとして使い、元のデータはdataフィールドへ しまっておけばよいでしょう。
$ java RunBinSort