algorithm b

アルゴリズムb 第3回

シェルソート

挿入ソートを変形したアルゴリズム(p.306, Fig 13.1 「シェルソートの原理」参照)。実用上、性能がよい。$O(n^{2.5})$ 〜 $O(n^{1.5})$

シェルソートのアイディア

挿入ソートは、ほとんど整列されているデータを速く整列できる。
前処理によってデータの整列度を高めておいてから挿入ソートを使えば
高速にソートができるはずである。

増分(h)の選び方

シェルソートの定義

減少数列 h = h₁, h₂, ..., h_l-1, h_l
(ただし h_l = 1) にしたがって 「h-ソート」を行う整列法。
"h-ソート (h-sort)" とは「hだけ離れた要素同士をソートすること」。

「整数 $x$, $y$ に関して $x > y$ であれば、『$x$-ソート』後『$y$-ソート』を行えば、データは『$x$-ソート済み』かつ『$y$-ソート済み』の性質を満たす」が一般に成り立つ。したがって、最終的に$1$ になるものであれば任意の減少数列を選ぶことができる。

ただし、次の性質には注意が必要である。

減少数列の性質

数列に現れる値は、互いに倍数になっていない方がよい。→理由はp.311 fig.13.2

どのような減少数列を用いると最良の結果が得られるかは、わかっていません。しかし、Knuth が解析＆実験的に求めたところ
$h_i = 3 \times h_{i+1} + 1$
とすれば、よい結果 $O(n^{1.25})$ が得られることがわかりました。
$h_i = \mbox{「} 2^i -1 \mbox{の逆順」}$
とすると $O(n^{1.5})$ となることは証明されています。

教科書のプログラム(p.313, List13.1)では、Knuthの「$h \leftarrow 3 * h + 1$ の逆順」を使って $h$ を $121$, $40$, $13$, $4$, $1$ と変化させる方法を採用しています。 $h$ を求める際に $n/9$ を越えない間、 $h \leftarrow 3*h+1$ を計算しています。「$n/9$ を越えない」ようにしているのは、極端に離れた要素を $h$-ソートしてもあまり高速化されず、むしろ欠点(余分な手間が増える)の方が大きいためです。

$h$ が $1$ より大きい値となるためには、$h$ の初期値の計算で 1 < a.length / 9 が成り立てばいいので a.length ≥ 18 となります(整数で計算することに注意)。データの個数を 18 個にして動作させてみます。

ShellSort.javaの実行例

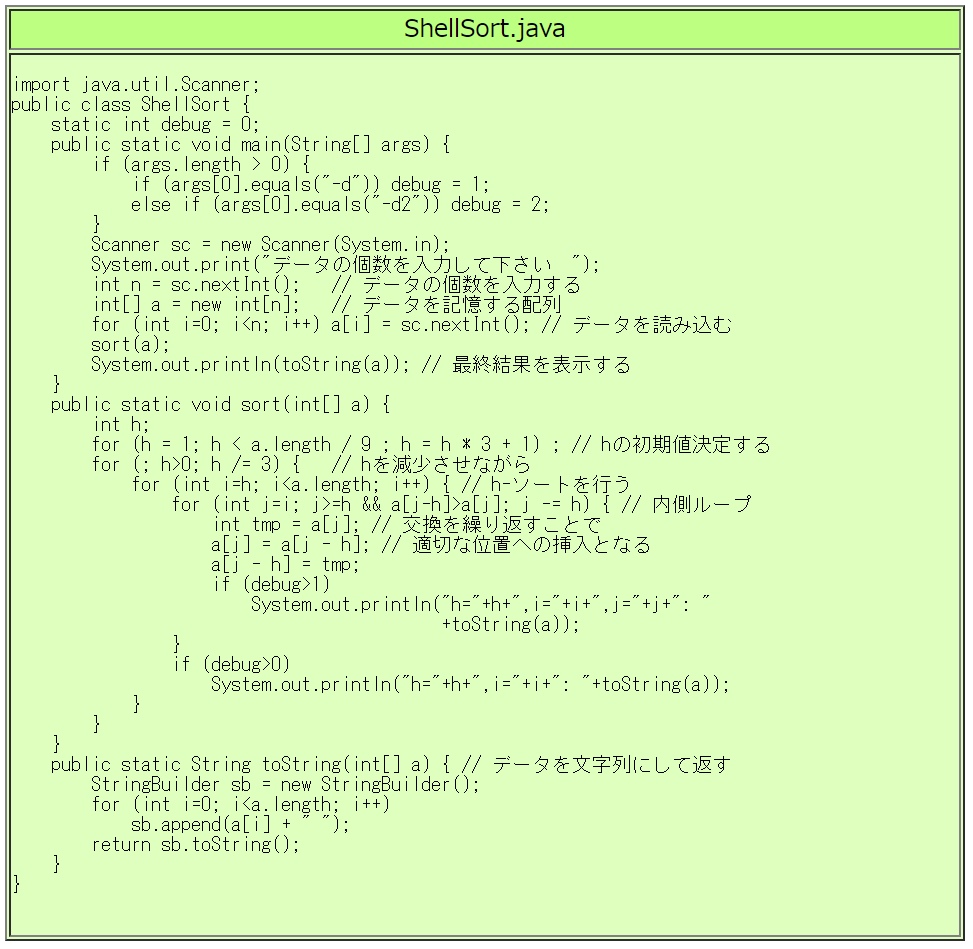
$ javac ShellSort.java   
$ java ShellSort -d   
データの個数を入力して下さい  18   
11 3 16 7 13 4 9 17 2 5 12 8 15 1 18 10 6 14   
h=4,i=4: 11 3 16 7 13 4 9 17 2 5 12 8 15 1 18 10 6 14 
h=4,i=5: 11 3 16 7 13 4 9 17 2 5 12 8 15 1 18 10 6 14 
h=4,i=6: 11 3 9 7 13 4 16 17 2 5 12 8 15 1 18 10 6 14 
h=4,i=7: 11 3 9 7 13 4 16 17 2 5 12 8 15 1 18 10 6 14 
h=4,i=8: 2 3 9 7 11 4 16 17 13 5 12 8 15 1 18 10 6 14 
h=4,i=9: 2 3 9 7 11 4 16 17 13 5 12 8 15 1 18 10 6 14 
h=4,i=10: 2 3 9 7 11 4 12 17 13 5 16 8 15 1 18 10 6 14 
h=4,i=11: 2 3 9 7 11 4 12 8 13 5 16 17 15 1 18 10 6 14 
h=4,i=12: 2 3 9 7 11 4 12 8 13 5 16 17 15 1 18 10 6 14 
h=4,i=13: 2 1 9 7 11 3 12 8 13 4 16 17 15 5 18 10 6 14 
h=4,i=14: 2 1 9 7 11 3 12 8 13 4 16 17 15 5 18 10 6 14 
h=4,i=15: 2 1 9 7 11 3 12 8 13 4 16 10 15 5 18 17 6 14 
h=4,i=16: 2 1 9 7 6 3 12 8 11 4 16 10 13 5 18 17 15 14 
h=4,i=17: 2 1 9 7 6 3 12 8 11 4 16 10 13 5 18 17 15 14 
h=1,i=1: 1 2 9 7 6 3 12 8 11 4 16 10 13 5 18 17 15 14 
h=1,i=2: 1 2 9 7 6 3 12 8 11 4 16 10 13 5 18 17 15 14 
h=1,i=3: 1 2 7 9 6 3 12 8 11 4 16 10 13 5 18 17 15 14 
h=1,i=4: 1 2 6 7 9 3 12 8 11 4 16 10 13 5 18 17 15 14 
h=1,i=5: 1 2 3 6 7 9 12 8 11 4 16 10 13 5 18 17 15 14 
h=1,i=6: 1 2 3 6 7 9 12 8 11 4 16 10 13 5 18 17 15 14 
h=1,i=7: 1 2 3 6 7 8 9 12 11 4 16 10 13 5 18 17 15 14 
h=1,i=8: 1 2 3 6 7 8 9 11 12 4 16 10 13 5 18 17 15 14 
h=1,i=9: 1 2 3 4 6 7 8 9 11 12 16 10 13 5 18 17 15 14 
h=1,i=10: 1 2 3 4 6 7 8 9 11 12 16 10 13 5 18 17 15 14 
h=1,i=11: 1 2 3 4 6 7 8 9 10 11 12 16 13 5 18 17 15 14 
h=1,i=12: 1 2 3 4 6 7 8 9 10 11 12 13 16 5 18 17 15 14 
h=1,i=13: 1 2 3 4 5 6 7 8 9 10 11 12 13 16 18 17 15 14 
h=1,i=14: 1 2 3 4 5 6 7 8 9 10 11 12 13 16 18 17 15 14 
h=1,i=15: 1 2 3 4 5 6 7 8 9 10 11 12 13 16 17 18 15 14 
h=1,i=16: 1 2 3 4 5 6 7 8 9 10 11 12 13 15 16 17 18 14 
h=1,i=17: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 
[nitta@ni java]$ java ShellSort -d2   
データの個数を入力して下さい  18   
11 3 16 7 13 4 9 17 2 5 12 8 15 1 18 10 6 14   
h=4,i=4: 11 3 16 7 13 4 9 17 2 5 12 8 15 1 18 10 6 14 
h=4,i=5: 11 3 16 7 13 4 9 17 2 5 12 8 15 1 18 10 6 14 
h=4,i=6,j=6: 11 3 9 7 13 4 16 17 2 5 12 8 15 1 18 10 6 14 
h=4,i=6: 11 3 9 7 13 4 16 17 2 5 12 8 15 1 18 10 6 14 
h=4,i=7: 11 3 9 7 13 4 16 17 2 5 12 8 15 1 18 10 6 14 
h=4,i=8,j=8: 11 3 9 7 2 4 16 17 13 5 12 8 15 1 18 10 6 14 
h=4,i=8,j=4: 2 3 9 7 11 4 16 17 13 5 12 8 15 1 18 10 6 14 
h=4,i=8: 2 3 9 7 11 4 16 17 13 5 12 8 15 1 18 10 6 14 
h=4,i=9: 2 3 9 7 11 4 16 17 13 5 12 8 15 1 18 10 6 14 
h=4,i=10,j=10: 2 3 9 7 11 4 12 17 13 5 16 8 15 1 18 10 6 14 
h=4,i=10: 2 3 9 7 11 4 12 17 13 5 16 8 15 1 18 10 6 14 
h=4,i=11,j=11: 2 3 9 7 11 4 12 8 13 5 16 17 15 1 18 10 6 14 
h=4,i=11: 2 3 9 7 11 4 12 8 13 5 16 17 15 1 18 10 6 14 
h=4,i=12: 2 3 9 7 11 4 12 8 13 5 16 17 15 1 18 10 6 14 
h=4,i=13,j=13: 2 3 9 7 11 4 12 8 13 1 16 17 15 5 18 10 6 14 
h=4,i=13,j=9: 2 3 9 7 11 1 12 8 13 4 16 17 15 5 18 10 6 14 
h=4,i=13,j=5: 2 1 9 7 11 3 12 8 13 4 16 17 15 5 18 10 6 14 
h=4,i=13: 2 1 9 7 11 3 12 8 13 4 16 17 15 5 18 10 6 14 
h=4,i=14: 2 1 9 7 11 3 12 8 13 4 16 17 15 5 18 10 6 14 
h=4,i=15,j=15: 2 1 9 7 11 3 12 8 13 4 16 10 15 5 18 17 6 14 
h=4,i=15: 2 1 9 7 11 3 12 8 13 4 16 10 15 5 18 17 6 14 
h=4,i=16,j=16: 2 1 9 7 11 3 12 8 13 4 16 10 6 5 18 17 15 14 
h=4,i=16,j=12: 2 1 9 7 11 3 12 8 6 4 16 10 13 5 18 17 15 14 
h=4,i=16,j=8: 2 1 9 7 6 3 12 8 11 4 16 10 13 5 18 17 15 14 
h=4,i=16: 2 1 9 7 6 3 12 8 11 4 16 10 13 5 18 17 15 14 
h=4,i=17: 2 1 9 7 6 3 12 8 11 4 16 10 13 5 18 17 15 14 
h=1,i=1,j=1: 1 2 9 7 6 3 12 8 11 4 16 10 13 5 18 17 15 14 
h=1,i=1: 1 2 9 7 6 3 12 8 11 4 16 10 13 5 18 17 15 14 
h=1,i=2: 1 2 9 7 6 3 12 8 11 4 16 10 13 5 18 17 15 14 
h=1,i=3,j=3: 1 2 7 9 6 3 12 8 11 4 16 10 13 5 18 17 15 14 
h=1,i=3: 1 2 7 9 6 3 12 8 11 4 16 10 13 5 18 17 15 14 
h=1,i=4,j=4: 1 2 7 6 9 3 12 8 11 4 16 10 13 5 18 17 15 14 
h=1,i=4,j=3: 1 2 6 7 9 3 12 8 11 4 16 10 13 5 18 17 15 14 
h=1,i=4: 1 2 6 7 9 3 12 8 11 4 16 10 13 5 18 17 15 14 
h=1,i=5,j=5: 1 2 6 7 3 9 12 8 11 4 16 10 13 5 18 17 15 14 
h=1,i=5,j=4: 1 2 6 3 7 9 12 8 11 4 16 10 13 5 18 17 15 14 
h=1,i=5,j=3: 1 2 3 6 7 9 12 8 11 4 16 10 13 5 18 17 15 14 
h=1,i=5: 1 2 3 6 7 9 12 8 11 4 16 10 13 5 18 17 15 14 
h=1,i=6: 1 2 3 6 7 9 12 8 11 4 16 10 13 5 18 17 15 14 
h=1,i=7,j=7: 1 2 3 6 7 9 8 12 11 4 16 10 13 5 18 17 15 14 
h=1,i=7,j=6: 1 2 3 6 7 8 9 12 11 4 16 10 13 5 18 17 15 14 
h=1,i=7: 1 2 3 6 7 8 9 12 11 4 16 10 13 5 18 17 15 14 
h=1,i=8,j=8: 1 2 3 6 7 8 9 11 12 4 16 10 13 5 18 17 15 14 
h=1,i=8: 1 2 3 6 7 8 9 11 12 4 16 10 13 5 18 17 15 14 
h=1,i=9,j=9: 1 2 3 6 7 8 9 11 4 12 16 10 13 5 18 17 15 14 
h=1,i=9,j=8: 1 2 3 6 7 8 9 4 11 12 16 10 13 5 18 17 15 14 
h=1,i=9,j=7: 1 2 3 6 7 8 4 9 11 12 16 10 13 5 18 17 15 14 
h=1,i=9,j=6: 1 2 3 6 7 4 8 9 11 12 16 10 13 5 18 17 15 14 
h=1,i=9,j=5: 1 2 3 6 4 7 8 9 11 12 16 10 13 5 18 17 15 14 
h=1,i=9,j=4: 1 2 3 4 6 7 8 9 11 12 16 10 13 5 18 17 15 14 
h=1,i=9: 1 2 3 4 6 7 8 9 11 12 16 10 13 5 18 17 15 14 
h=1,i=10: 1 2 3 4 6 7 8 9 11 12 16 10 13 5 18 17 15 14 
h=1,i=11,j=11: 1 2 3 4 6 7 8 9 11 12 10 16 13 5 18 17 15 14 
h=1,i=11,j=10: 1 2 3 4 6 7 8 9 11 10 12 16 13 5 18 17 15 14 
h=1,i=11,j=9: 1 2 3 4 6 7 8 9 10 11 12 16 13 5 18 17 15 14 
h=1,i=11: 1 2 3 4 6 7 8 9 10 11 12 16 13 5 18 17 15 14 
h=1,i=12,j=12: 1 2 3 4 6 7 8 9 10 11 12 13 16 5 18 17 15 14 
h=1,i=12: 1 2 3 4 6 7 8 9 10 11 12 13 16 5 18 17 15 14 
h=1,i=13,j=13: 1 2 3 4 6 7 8 9 10 11 12 13 5 16 18 17 15 14 
h=1,i=13,j=12: 1 2 3 4 6 7 8 9 10 11 12 5 13 16 18 17 15 14 
h=1,i=13,j=11: 1 2 3 4 6 7 8 9 10 11 5 12 13 16 18 17 15 14 
h=1,i=13,j=10: 1 2 3 4 6 7 8 9 10 5 11 12 13 16 18 17 15 14 
h=1,i=13,j=9: 1 2 3 4 6 7 8 9 5 10 11 12 13 16 18 17 15 14 
h=1,i=13,j=8: 1 2 3 4 6 7 8 5 9 10 11 12 13 16 18 17 15 14 
h=1,i=13,j=7: 1 2 3 4 6 7 5 8 9 10 11 12 13 16 18 17 15 14 
h=1,i=13,j=6: 1 2 3 4 6 5 7 8 9 10 11 12 13 16 18 17 15 14 
h=1,i=13,j=5: 1 2 3 4 5 6 7 8 9 10 11 12 13 16 18 17 15 14 
h=1,i=13: 1 2 3 4 5 6 7 8 9 10 11 12 13 16 18 17 15 14 
h=1,i=14: 1 2 3 4 5 6 7 8 9 10 11 12 13 16 18 17 15 14 
h=1,i=15,j=15: 1 2 3 4 5 6 7 8 9 10 11 12 13 16 17 18 15 14 
h=1,i=15: 1 2 3 4 5 6 7 8 9 10 11 12 13 16 17 18 15 14 
h=1,i=16,j=16: 1 2 3 4 5 6 7 8 9 10 11 12 13 16 17 15 18 14 
h=1,i=16,j=15: 1 2 3 4 5 6 7 8 9 10 11 12 13 16 15 17 18 14 
h=1,i=16,j=14: 1 2 3 4 5 6 7 8 9 10 11 12 13 15 16 17 18 14 
h=1,i=16: 1 2 3 4 5 6 7 8 9 10 11 12 13 15 16 17 18 14 
h=1,i=17,j=17: 1 2 3 4 5 6 7 8 9 10 11 12 13 15 16 17 14 18 
h=1,i=17,j=16: 1 2 3 4 5 6 7 8 9 10 11 12 13 15 16 14 17 18 
h=1,i=17,j=15: 1 2 3 4 5 6 7 8 9 10 11 12 13 15 14 16 17 18 
h=1,i=17,j=14: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 
h=1,i=17: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

h=4のときの動作は、データの列を4で割った余りで分類してみると理解しやすくなります。

       i-h          i →iを増やして行く
       ↓          ↓
index:  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
-------------------------------------------------------------
余り0: 11          13           2          15           6
余り1:     3           4           5           1          14
余り2:       16           9          12          18
余り3:           7          17           8          10

a.length<18のとき	a.length/9=0 or 1	h=1のまま
a.length=18のとき	a.length/9=2	h=4
a.length=45のとき	a.length/9=5	h=13
a.length=126のとき	a.length/9=14	h=40
a.length=369のとき	a.length/9=41	h=121
a.length=1098のとき	a.length/9=122	h=364
a.length=3285のとき	a.length/9=365	h=1093
a.length=9846のとき	a.length/9=1094	h=3280
a.length=29529のとき	a.length/9=3281	h=9841

InsertSort.javaの実行例と見比べて、動作の似ている部分と、異なる部分についてよく理解して下さい。

単純なソートは、非常に要素数が少い(数十個とか)場合にのみ使うことができます。要素数が多い場合(多過ぎないとき)は、シェルソートを使うべきです。また、要素数が非常に多い場合(1000以上とか)は、クイックソートを使うべきです。

アルゴリズムA 演習

作成したプログラムが正しく動作することを確認したら、それぞれの提出先に提出しなさい。提出した後は、正しく提出されていることを http://ynitta.com/class/algoB/local/handin/ で必ず確認しておいて下さい。提出〆切は次回の講義の開始時刻です。

課題3a: ShellSortのプログラムを動かしてみる

提出ファイル	ShellSort.java
コメント欄:	dec400k.txt, inc400k.txt, dec400k.txtそれぞれに対する「シェルソートと挿入ソートの計算時間と、シェルソートの速度が挿入ソートの何倍か」
提出先:	「宿題提出Web:アルゴリズムA：課題3a」 http://ynitta.com/class/algoB/local/handin/up.php?id=kadai3a

http://ynitta.com/class/algoB/sortdata/ の下に、次の入力仕様を満たす3種類のデータが置いてあります。

rand400k.txt -- 400000個のデータがランダムに並んでいる
inc400k.txt -- 400000個のデータが昇べきの順に並んでいる
dec400k.txt -- 400000個のデータが降べきの順に並んでいる

これらの中のデータは最小値が $0$ 以上で最大値が $999999$ 以下であることが保証されています。 (課題1aや2aで使った http://ynitta.com/class/algoB/sortdata/*200k.txt と比較すると、データの個数が2倍、最大値は10倍のデータです。)

InsertSort.javaとShellSort.javaがこれらの3種類のデータを処理するのに必要な時間をそれぞれ計測し、答えなさい。さらにShellSort.javaの処理速度がInsertSort.javaの何倍であるかを 3種類のデータ毎に答えなさい。

課題3b: ShellSortにおけるデータの交換回数

提出ファイル	ShellSort2.java
コメント欄:	3種類のデータ対するデータ交換の回数
提出先:	「宿題提出Web:アルゴリズムA：課題3b」 http://ynitta.com/class/algoB/local/handin/up.php?id=kadai3b

ShellSort.javaを変更して、sort()メソッドの中でデータの交換が何回行われたかを記録しておくようにしましょう。そして、その回数を返すメソッド static long getCount() を新たに追加して下さい。ファイル名はShellSort2.javaとしましょう。上記の3種類のデータに対して動作させて、それぞれsort()の中でデータ交換が何回行われたかを調べて下さい。

CountShellSort.javaの実行例

% javac CountShellSort.java   
% java CountShellSort < rand400k.txt   
ここに表示される交換回数を答えなさい。
% java CountShellSort < inc400k.txt   
ここに表示される交換回数を答えなさい。
% java CountShellSort < dec400k.txt   
ここに表示される交換回数を答えなさい。

課題3c: 挿入ソートにおけるデータの交換回数

提出ファイル	InsertSort2.java
コメント欄:	データ交換の回数およびShellSort2.javaの何倍か
提出先:	「宿題提出Web:アルゴリズムA：課題3c」 http://ynitta.com/class/algoB/local/handin/up.php?id=kadai3c

InsertSort.javaを変更して課題3bと同等な機能を追加し、ファイル名をInsertSort2.javaとして下さい。 InsertSortの中で、 rand400k.txt, inc400k.txt, dec400k.txt のそれぞれに対してデータ交換が何回行われるか計測し、答えなさい。さらに、それぞれのデータに対して、InsertSortはShellSortの何倍多くデータを交換しているかを答えなさい。(0/0の場合は1と答えればよいものとします)

CountInsertSort.javaの実行例

% javac CountInsertSort.java   
$ java CountInsertSort < rand400k.txt   
ここに表示される交換回数を答えなさい。
$ java CountInsertSort < inc400k.txt   
ここに表示される交換回数を答えなさい。
$ java CountInsertSort < dec400k.txt   
ここに表示される交換回数を答えなさい。

[注意]

データの交換回数を記録しておく整数型の変数の型は、 4byte (= 32bit) 幅の int 型では駄目で 8byte (= 64bit) 幅の long 型でなければならない。

int型は32bitで符号(正負)があるため、表現可能な正の最大値は $2^{31} - 1$ である。 $2^{10}$ が約 $10^3$ (正確には $1024$ )であることから、 $2^{31}$ では約 $2 \times 10^9$ までの正の整数しか表せないことがわかる。

今回扱っているデータの個数は $400,000$ なので、 $O(n^2)$ のアルゴリズムでは、 $400,000^2 = 1.6 \times 10^{11}$ 回のオーダーの比較が起こり得る。