アルゴリズムb 第1回

整列

データ (レコードと呼ぶことがあります) の集まりを、 キーの値の大小関係によって並べ換える操作。

• 並び順
• キーの大きい方が後 ... 昇順
• キーの小さい方が後 ... 降順
• データの置き場所
• 内部整列 (internal sort):
すべてのデータを主記憶状に置いてソートする。→ランダムアクセスが可能
• 外部整列 (external sort):
一部のデータだけは主記憶状に置くが、残りの大部分は(ハードディスクなどの) ２次記憶上にいてソートする。→シーケンシャルアクセスが前提

注意

比較によらない整列もある(デジタルソート→教科書17章)。 この方法の整列には、 binソート、分布数え上げソート、基数ソートなどがある。 キーの範囲をある範囲に限定すると、 計算量が $O(n)$ となるものも存在する。

ちなみに、比較による整列では最速のアルゴリズムでも $O( n \log n )$ かかる。

計算量

nの値に応じて、次のように使い分けるとよいらしい。

安定な整列

「安定な整列」＝「整列するデータの中に同じキーを持つものがあったとき、 それらの順番が整列後でも保たれる」。(p.287, Fig.11.2参照)

単純な整列アルゴリズムである 「選択ソート」、「バブルソート」、「挿入ソート」 のうち、選択ソートは「安定な整列」ではありませんが、 「バブルソート」と「挿入ソート」は「安定な整列」です。 選択ソートが安定でないことは8 5 5 2 1のような5個のデータを昇順(小さい順)に整列する状況を考えればわかります。

一般に、「単純で遅い→安定」、「複雑で速い→安定でない」傾向があります。 しかし、「本来のキー」以外に「データの元の位置」をサブキーとして使い、 「本来のキー」が等しいときはサブキーを比較するようにすれば、 (余分なキーの比較というオーバーヘッドは発生するが)本来「安定でない」 アルゴリズムを「安定」として使うことができます。

Javaのクラス

java.util.Arraysクラスは「配列」を扱うためのクラスだが、 昇順に並べ変えるsort()メソッドが用意されていている。

単純な整列アルゴリズム

選択ソート(p.297)、バブルソート(p.294)、挿入ソート(p.300)の３種類が単純なソート $O(n^2)$ です。 選択ソートに関して今回説明します。

選択ソート

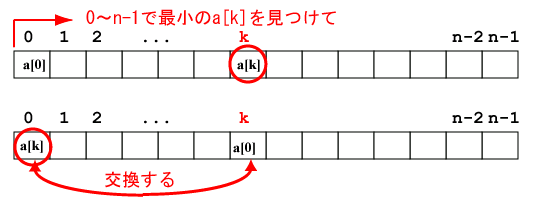
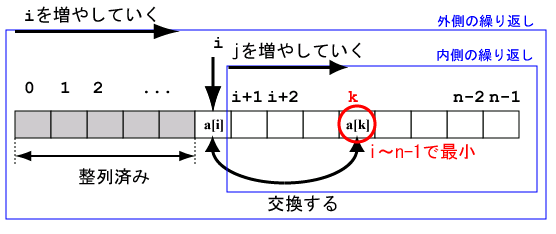
        n個の値  a[0], a[1], ..., a[n-1] を並べ替えるには、まず全体を
	見渡してその中で最小のものを見つけ、それをa[0]と交換する。
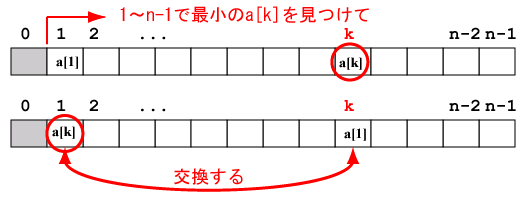
        つぎに、a[1],a[2],...,a[n-1]の中で最小のものを見つけ、それを
        a[1]と交換する。以下同様に続ける。

1. n個の要素を持つ配列があるとします



2. インデックスが 0 〜 n-1 の範囲で最小の値を持つ a[k] を探します。そして、a[0] と a[k] を交換します。



3. 左端の1個要素だけが整列が終った状態になります。



4. インデックスが 1 〜 n-1 の範囲で最小の値を持つ a[k] を探します。そして、a[1] と a[k] を交換します。



5. 左端の２個の要素だけが整列が終った状態になります。



6. これを」繰り返します。
7. 最終的に全体の整列が終った状態になります。

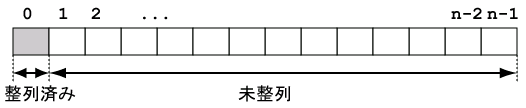
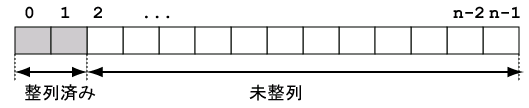
一般に左端の i 個の要素の整列が終った状態では、 i 〜 n-1 の範囲で最小の値を持つ a[k] を探し、 a[i] と a[k] を交換すればよいことがわかるでしょう。

この方針に基づいて Sort1.java を作成してみましょう。 入力データは、整数とし、まず最初にデータの個数が 入力されるものとします。

sp204: ~/pro 4> javac Sort1.java 
sp204: ~/pro 5> java Sort1 
データの個数を入力して下さい  8 
5 8 7 9 2 7 1 3 
1 2 3 5 7 7 8 9         ←小さい順に表示される
sp204: ~/pro 6> 

アルゴリズムb 演習

作成したプログラムが正しく動作することを確認したら、それぞれの 提出先に提出しなさい。

提出した後は、正しく提出されていることを http://ynitta.com/class/algoB/local/handin/ で必ず確認しておいて下さい。

課題提出〆切は、次回の授業開始時刻です。

課題1a: 選択ソート

Sort1.javaにおいて「配列内のデータを整列」させる部分や「配列内のデータを表示」 させる部分をメソッドにしたプログラムを作成して下さい。 これらのメソッドへの引数としては、処理すべき配列を渡すことになります。 ファイル名は SelectionSort.javaとして下さい。

$ javac SelectionSort.java   
$ java SelectionSort   
データの個数を入力して下さい  8   
5 8 7 9 2 7 1 3               ←入力データ
1 2 3 5 7 7 8 9            ←結果の出力 
$ java SelectionSort -d       ←コマンド引数に-dをつけて実行すると
データの個数を入力して下さい  8   
5 8 7 9 2 7 1 3               ←入力データ
sorting: 1 8 7 9 2 7 5 3   ←途中結果を出力する  
sorting: 1 2 7 9 8 7 5 3 
sorting: 1 2 3 9 8 7 5 7 
sorting: 1 2 3 5 8 7 9 7 
sorting: 1 2 3 5 7 8 9 7 
sorting: 1 2 3 5 7 7 9 8 
sorting: 1 2 3 5 7 7 8 9 
1 2 3 5 7 7 8 9              ←結果の出力

課題1b: 中央値

複数の整数値を入力として、中央値(median)を出力するプログラムを書きなさい。

[注] 中央値 (median)とは、有限個のデータを小さい順に並べたとき中央に位置する値である。 たとえば5人の人がいるとき、その5人の年齢の中央値は3番目に年寄りな人の年齢である。 ただし、データが偶数個の場合は、中央に近い2つの値の算術平均をとる。

[注] もしもソートが必要ならば、今回作成した SelectionSortクラスの SelectionSort.sort(int[]) メソッドを利用すること。

$N$ はデータの個数を表す自然数。 $D_i$ は $0$ 以上 $100$ 以下の整数。

5
80
30
70
90
40

6
80
30
70
90
40
60

6
80
30
70
90
40
65

$ javac GetMedian.java 
$ java GetMedian < intdata01.txt 
70
$ java GetMedian < intdata02.txt 
65
$ java GetMedian < intdata03.txt 
67.5