アルゴリズムA 第4回

基本的なデータ構造

リスト

「リスト(list)」というデータ構造は、通常、次のような構造を表します。

しかし、教科書では、上記の構造を「連結リスト」と呼び、 「リスト」という語を「データを線形に並べたもの」とか「一覧表」 などという意味で使用しているようです。混乱しないように注意して下さい。

リストに対する操作

配列による実現

    int[] x = new int[データの最大個数];

k番目に要素を挿入するには、それよりも後ろの要素を全て 1ずつずらしてコピーする必要があります。 要素の個数がn個だとすると、ずらすべき要素の個数は平均で n/2 となるので、要素を1個挿入するための計算量はO(n) です。

k番目の要素を削除するための計算量も、同様にO(n)と なります。

k番目の要素を読み書き(アクセス)するには k[i] でいいので、計算量はO(1)となります。

結論として、リストへの要素の挿入や削除が多く発生する場合、 配列は適切な実現方法ではないことになります。

スタック

「挿入と削除がリストの先頭のみで行われるもの」が「スタック (stack)」です。

スタックでは、リストの先頭をtop, 最後をbottomと呼びます。 「topにデータを挿入すること」を push, 「topからデータを取り出すこと」を popと呼びます。

「最初に挿入されたデータが最後に取り出される」ために "First In, Last Out" と呼ぶことがあります。 もちろん、逆の見方をすれば 「最後に挿入されたデータが最初に取り出される」ことになるので "Last In, First Out" とも言います。

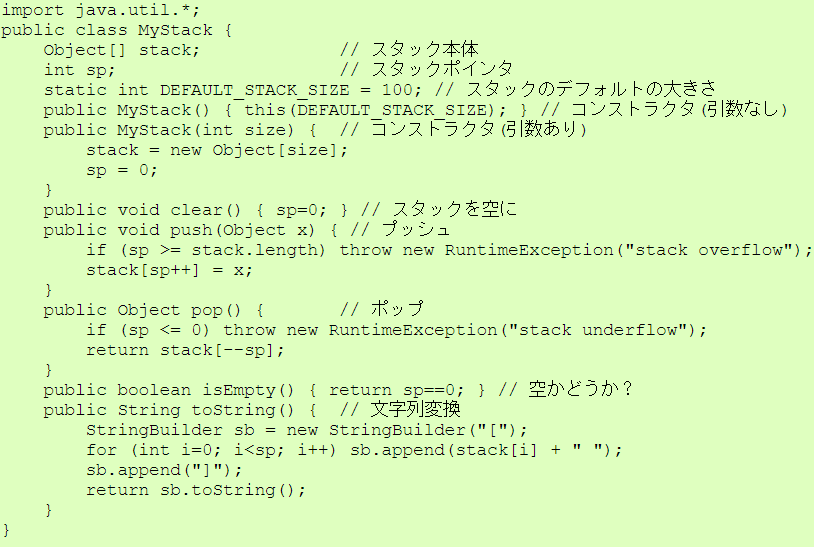
MyStack.java

RunMyStack.java

$ javac RunMyStack.java 
$ java RunMyStack 
[a b c ]
pop: c
[a b ]
[a b d e f ]
pop: f
pop: e
pop: d
pop: b
pop: a
[]

逆ポーランド記法

式 $(a + b) \times (c - d)$ を括弧を使わずに読み上げてみましょう。 もし、「$a$ 足す $b$ かける $c$ 引く $d$ 」 と読み上げると $ a + b \times c - d$ との区別がつかなくなってしまいます。 このような場合は、「演算子をデータの後から読み上げる」 方法を取るとうまくいきます。 つまり 「$a$ と $b$ を足したもの に $c$ から $d$ を引いたものを掛けたもの」 と表現すると括弧を使わずにうまく表現できます。

このような、「データを先に書いて、演算子を後に書く方法」を、 『後置記法 (postfix notation)』とか『逆ポーランド記法 (reverse polish notation)』などと呼びます。 逆ポーランド記法を用いると、上記の例は 「$a$ $b$ $＋$ $c$ $d$ $−$ $\times$」 と表現されます。 式を表すのに括弧が不要なので「演算式の処理が簡単である」 という利点が逆ポーランド記法にはあります。

ちなみに、 式 $(a + b) \times (c - d)$ のような通常の記法を挿入記法 (infix notation)と呼びます。

逆ポーランド記法で表現された式を処理するときは

• データが入力されると、スタックにpushする
• 演算子が入力されると、スタックから２個データをpopして演算を行い、 計算結果をスタックにpushする

例として (3 + 5) * (7 - 1) という式が逆ポーランド記法で 表されたときに、スタックを使ってどのように処理できるか 見てみましょう。

挿入記法:              (3 + 5) * (7 - 1)
逆ポーランド記法:      3 5 + 7 1 - *

Calculator.java

$ javac Calculator.java 
$ java Calculator 
3 5 + 7 1 - * 
答は48です。
6 3 - 2 5 + 8 4 - - * 
答は9です。
Ctl-D   ←入力行の先頭でコントロールキーとDを同時に押すと入力終了。
$ java Calculator 
2 3 5 + 
入力された式が不正です。
2 3 + 5 - * 
Exception in thread "main" java.lang.RuntimeException: stack underflow
	at MyStack.pop(MyStack.java:17)
	at Calculator.pop(Calculator.java:8)
	at Calculator.main(Calculator.java:30)

アルゴリズムa 演習

課題提出〆切は次回の講義の開始時刻です。

課題4a

Calculator.java を次のデータに対して動作させて下さい (注意: Calculator.javaの実行にはMyStack.javaも必要です)。

[データ1]
73  26  *  5  10  +  27  103  19  -  *  -  -
[データ2]
21  17  5  203  32  -  2  3  5  *  *  +  -  -  108  9  /  +
[データ3]
21  17  5  203  32  -  2  3  5  *  *  +  -  -  108  9  /  -  +

課題4b

課題4aで作成した Calculator.java を参考にして、 実数を扱えるようにしたCalculator2.javaを作成しなさい。 すべての計算は実数で行えばよいものとします。

コメント欄には実行結果を貼り付けておいて下さい。

$ javac Calculator2.java 
$ java Calculator2 
3 2 + 
答は5.0です。
3.2 2.5 + 8.3 7.8 - * 
答は2.850000000000005です。
5 5 * 3.14 * 1.5 / 
答は52.333333333333336です。
$