アルゴリズムa 第2回

線形探索の計算量は $O(n)$ ですが、二分探索法 (Binary Search) の 計算量は $O(\log n)$ です。

二分探索法では、データは大きい順番、または小さい順番に並んでいます。 注目する領域の真中のデータが、探索するデータよりも大きいか、小さいかで 探索領域を次々に半分にしていきます。

二分探索法で10個のデータから、「14」というデータを探索する様子を 下に示します。 表の中では、注目する領域の下が l (low), 上が h (high)、 真中が m (middle) で表されています。

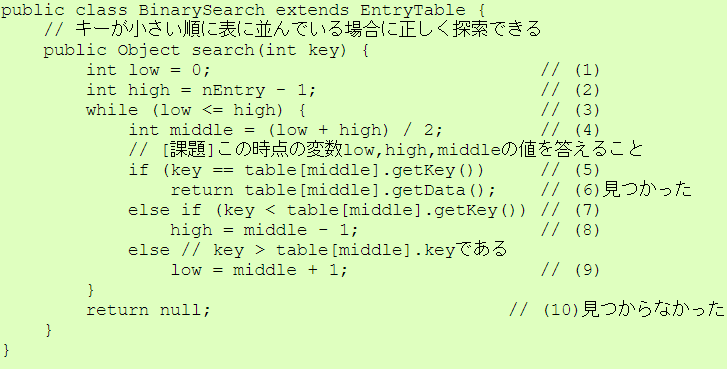
下に示す BinarySearch.java のプログラムにおいて、探索の部分の 計算量を考えてみましょう。

繰り返しの回数は以下のように計算できます。

データの総数を $n$ とおくと、繰り返しの度に high と low で囲む領域は
半分になりますから、繰り返し回数を $m$ とすると
$\quad 2^m = n$
両辺の $\log_e$ を計算すると
$\displaystyle \quad m \log_e 2 = \log_e n$
$\displaystyle \quad \therefore ~~ m = \frac{\log_e n}{\log_e 2}$

$\log_e 2$ は定数なので、繰り返しの回数は $\log n$ のオーダーになります。

二分探索法による探索の計算量

二分探索法 BinarySearch.java

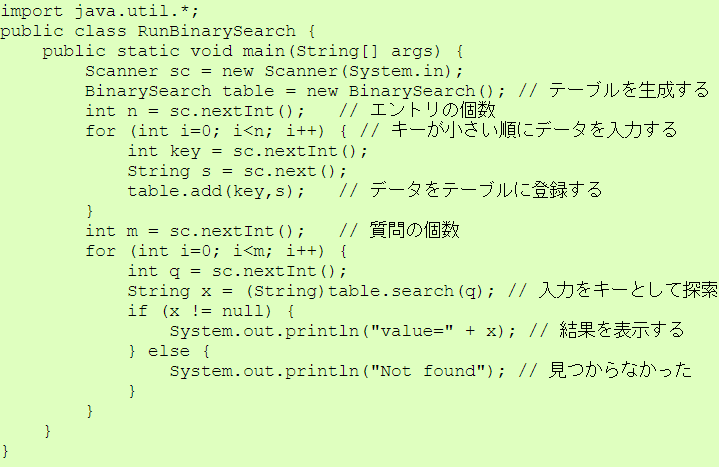
RunBinarySearch.java

% javac RunBinarySearch.java
% java RunBinarySearch
10
2 two
4 four
5 five
8 eight
13 thirteen
14 fourteen
18 eighteen
20 twenty
21 twenty-one
26 twenty-six
4
1
Not found
32
Not found
3
Not found
20
value=twenty

RunBinarySearch.javaへの入力形式

最初の行には1個の整数 $N$ が含まれる。 $N$ はデータの数 (ただし $1 \leqq N \leqq 100$ ) を表す。

2行目以降は $N$ 行に渡ってデータが続く。 各行は 「1個の整数 $K_i$」、 「データの区切りとしての1個の空白文字」、 「1個の文字列 $D_i$」 を含む (ただし $1 \leqq i \leqq N$ )。 $K_i$ はデータのうち「比較の対象となるキー」であり、 $D_i$ は「それ以外のデータ」である。

ただし$i \lt j$ ならば $K_i \leqq K_j$ が成り立つとする(つまりキーが小さい方から大きい方に順に並んでいるデータが与えられる)。

その次の行は、質問の個数を表す整数 $M$ を含む( $1 \leqq M \leqq 10$ )。 それ以降に $M$ 行続き、各行は探索すべきキーとなる整数 $Q_j$ (ただし $1 \leqq j \leqq M$ ) を含む。

二分探索法のためのデータ登録の計算量

二分探索法では、データは大きさの順番に並んでいることが必要です。 したがって、データを登録する毎に以下の計算量が必要となります。

データを1個登録するには、$O(n)$ の計算量が必要です。 すなわち、データを $n$ 個登録するには、$O(n^2)$ の計算量が必要である、ということになります。

ただし、データを最初にまとめて登録する場合は、もう少し効率のよい方法が使えます。 データ1個をキーの大きさに関係なく(順番ばらばらに)登録する計算量は $O(1)$ なので、 $n$ 個のデータを順番ばらばらに登録する計算量は $O(n)$ となります。 最後に一度だけ整列(sort、最も効率のよいアルゴリズムだと$O(n \log n)$で可能)を行えば、 全体として $O(n \log n)$ で整列したデータ全体が得られます。

探索アルゴリズムの比較

データがn個の場合の計算量は、アルゴリズムによって以下のように 変化します。

一般に、データの探索回数の方が登録回数よりも多くなりますので、 そのような場合は線形探索法よりも二分探索法の方が効率がよくなります。 ただし、「探索途中で頻繁にデータの登録がある場合は、二分探索法は向かない」 ことになります。

適切なアルゴリズム

どのようなアルゴリズムが「適切である」かは、 データの大きさやプログラムの利用法によって異なります。 理由を以下に示します。

• nが小さいときは、オーダーの大小よりも定数係数の大小が 支配的要因となることがあります。
• 効率のよいアルゴリズムは複雑なプログラミングを必要としがちです。 実行時間だけではなくプログラミングの手間も考える必要があります。 使い捨てのプログラムに対してあまり凝っても仕方がありません。
• 時間と空間のトレードオフを考える必要があります。 時間的に効率のよいアルゴリズムは大きな空間を必要とする場合があり、 それを許容する実行環境が必要となります。

アルゴリズムA 演習

作成したプログラムが正しく動作することを確認したら、それぞれの 提出先に提出しなさい。 提出した後は、正しく提出されていることを http://nw.tsuda.ac.jp/class/algoA/local/handin/ で必ず確認しておいて下さい。 提出〆切は次回の講義の開始時刻です。

課題2a

RunBinarySearch.java を動作させて下さい。 Entry.java, EntryTable.java, BinarySearch.java, RunBinarySearch.java が必要となります。

10個の入力データと4個の質問のデータを

10 ←データの個数
2 two
4 four
5 five
8 eight
13 thirteen
14 fourteen
18 eighteen
20 twenty
21 twenty-one
26 twenty-six

4 ←質問の個数
1
32
3
20

	    // [課題]この時点の変数low,high,middleの値を答えること

BinarySearch.javaを提出して下さい。 ただし、提出する際のコメント欄には各質問に対する上記の考察の 結果を記述すること。

[解答例]
 質問のキー:6の場合
  4回通過する。
  low=0, high=9, middle=4
  low=0, high=3, middle=1
  low=2, high=3, middle=2
  low=3, high=3, middle=3

課題2b

与えられた実数 x の立方根(3乗根, 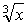)を計算するプログラムを作成しなさい。 与えられる実数 x の値は1より大きいと仮定して構わない。 答に含まれる誤差は1.0×10^-5よりも小さいこと。 ただし、Mathクラスのメソッドを使ってはならない。

(ヒント)2分法を使えばよい。 最初は low=1.0, high=x と置いて、lowとhighの真ん中 midの3乗と x を比較する。比較した結果、lowとhighの区間を1/2ずつ狭めていって high-lowが許容誤差よりも小さくなったら終了する。

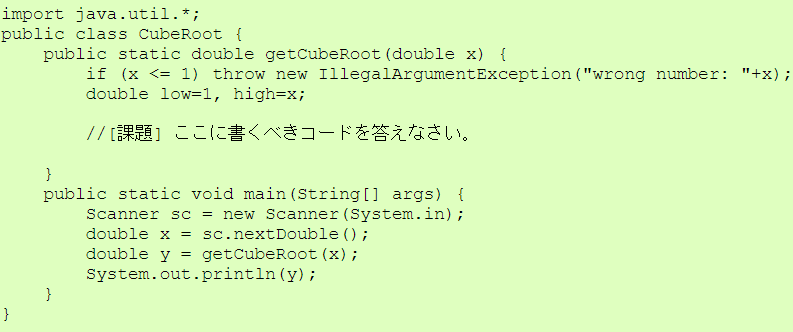
CubeRoot.java

$ javac CubeRoot.java 
$ java CubeRoot 
5 
1.7099723815917969
$ java CubeRoot 
64 
3.9999998211860657
$ java CubeRoot 
8 
1.9999995231628418

(例) 8 の3乗根として 1.9999995231628418 を得る計算過程