
データが n個あっても、上記の[手順2]の計算時間が一定であれば、 計算量は O(1)。
ただし、「衝突(異なるデータを同じ場所に登録しようとする)」 が起きた時の回避方法が必要となる。
| 用語 | 英語 | 説明 |
|---|---|---|
| ハッシュ表 | hash table | [手順1]の表 |
| バケット | bucket | ハッシュ表の中でデータを1個記憶する場所 |
| ハッシュ関数 | hash function | [手順2]の計算に使う関数 |
| ハッシュ値 | hash value | [手順2]の計算値 |
異なるデータに対して、同じハッシュ値が得られた場合。
| p.179 ハッシュ値の衝突例 |
|
探索:まず「ハッシュ値を計算してバケットの場所を求めて」、それから 「バケットに連結されているリストを線形探索する」。
データの追加・削除:まず「ハッシュ値を計算してバケットの場所を求めて」、 それから「連結リストの挿入・削除を行う」。
プログラム例(List8.2:p.181〜p.186, List8.3:p.188-189):
ハッシュ関数:
文字列のアスキーコードの和を求めて(MyKey.hash(): p.188 l.34-43)、
ハッシュ表の大きさで割った余り(HashC.hash(): p.183, l.68-71)
| 解析 |
|
バケットの数: $B$ データの総数: $N$ ハッシュ関数がデータを均等に振り分けると仮定すると、 $\displaystyle \quad \mbox{1個のバケットに登録されているデータの個数} = \frac{N}{B}$ 探索の計算量: $\displaystyle O(1 + \frac{N}{B})$ ハッシュの計算量: $\displaystyle O(1)$ 連結リストの線形探索: $\displaystyle O(\frac{N}{B})$ もしも、$B$ が $N$ よりもはるかに大きければ ($\displaystyle B>>N$)、 $\displaystyle \frac{N}{B}$ は(非常に小さいから)定数とみなせるので、全体の計算量は $O(1)$ とみなすことができる |
衝突が起きた時(ハッシュ値がぶつかった時)、再び別のハッシュ値を計算する。
| 最も簡単なハッシュ値の再計算方法: |
|
衝突したら、その次の(隣の)バケットを選ぶ。 もし、そこも埋まっていたらさらにその隣を選ぶ。 空きバケットを発見するまで、この手順を繰り返す。 $h_k(x) = (h(x) + k) \mod B$ |
ハッシュ表の大きさ=バケットの個数=10
データの総数=6個 (このうち5個のデータを登録する)
各データのハッシュ値を次の表のように仮定する。| データ | a | b | c | d | e | f |
|---|---|---|---|---|---|---|
| ハッシュ値 | 1 | 5 | 8 | 5 | 6 | 6 |
| インデックス | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 初期状態 | . | . | . | . | . | . | . | . | . | . |
| aを追加 | . | a | . | . | . | . | . | . | . | . |
| bを追加 | . | a | . | . | . | b | . | . | . | . |
| cを追加 | . | a | . | . | . | b | . | . | c | . |
| dを追加 | . | a | . | . | . | b | d | . | c | . |
| eを追加 | . | a | . | . | . | b | d | e | c | . |
dを追加したとき、バッシュ値は5であるが、すでにbが登録されている ので次(インデックスは6)に登録した。
eを追加したとき、バッシュ値は6であるが、すでにdが登録されている ので次(インデックスは7)に登録した。
| インデックス | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 現在の状態 | . | a | . | . | . | b | d | e | c | . |
bはハッシュ値5であるが、その場所で発見できる。
eはハッシュ値6であるが、その場所で発見できない。 その場合は次(隣)を探索し、7で発見できる
fはハッシュ値6であるが、その場所で発見できない。 次々と隣を(繰り返し)探索するが発見できない。 9に空のバケットがあるので、結局存在しないことがわかる(探索失敗)。
| インデックス | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 元の状態 | . | a | . | . | . | b | d | e | c | . |
| dを削除 | . | a | . | . | . | b | . | e | c | . |
| e,fの探索が変 | . | a | . | . | . | b | . | e | c | . |
| 改善方法 | . | a | . | . | . | b | 削除 | e | c | . |
dを登録してあるバケット(6)から単に削除してそのバケットを空にすると、 衝突したデータの探索が正しく動作しなくなる。 →削除した場合は、「空」ではなく「削除済み」という印を入れておく。 「削除済み」では探索を終了しない。
「ハッシュ値がぶつかったら次のバケットへ」という方針では、 データが塊になりやすい。
→「再ハッシュでバケットをランダムに選択する」とよい。
| 題名 |
|
ハッシュ表の大きさ(=バケットの数)がBであるとすると、 $1,2, ..., (B-1)$ を並び替えて $ n_1, n_2, \cdots , n_{B-1}$ とし、再計算を次の式で行う。 $h_k(x) = (h(x) + n_k) \mod B$ |
ハッシュ表の大きさ: B=10 とする。
ハッシュ値を再計算するための計算式に、次のような数字を 順番に使う。
| 再計算用オフセット | n1 | n2 | n3 | n4 | n5 | n6 | n7 | n8 | n9 |
| 値 | 6 | 1 | 4 | 7 | 2 | 9 | 8 | 3 | 5 |
| 再計算したハッシュ値 | h1(x) | h2(x) | h3(x) | h4(x) | h5(x) | h6(x) | h7(x) | h8(x) | h9(x) |
| h(x)=3の時 | 9 | 4 | 7 | 0 | 5 | 2 | 1 | 6 | 8 |
| h(x)=4の時 | 0 | 5 | 8 | 1 | 6 | 3 | 2 | 7 | 9 |
この方法を取ると「データの塊ができにくい」のが利点。
α = ハッシュ表の使用率 = 登録したデータ数/全バケット数
| 隣のバケットへ | ランダム数列で選んだバケットへ | |
|---|---|---|
| 発見できた場合 | $\displaystyle \frac{1 - \displaystyle \frac{\alpha}{2}}{1-\alpha}$ | $\displaystyle \frac{1}{\alpha} \log_e \frac{1}{1- \alpha}$ |
| 発見できずの場合 | $\displaystyle \frac{1}{2} + \frac{1}{2} (1-\alpha)^2$ | $\displaystyle \frac{1}{1- \alpha}$ |
| α | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 | 0.45 | 0.50 | 0.55 | 0.60 | 0.65 | 0.70 | 0.75 | 0.80 | 0.85 | 0.90 | 0.95 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 平均値 | 1.03 | 1.06 | 1.09 | 1.13 | 1.17 | 1.21 | 1.27 | 1.33 | 1.41 | 1.50 | 1.61 | 1.75 | 1.93 | 2.17 | 2.50 | 3.00 | 3.83 | 5.50 | 10.5 |
| α | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 | 0.45 | 0.50 | 0.55 | 0.60 | 0.65 | 0.70 | 0.75 | 0.80 | 0.85 | 0.90 | 0.95 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 平均値 | 1.03 | 1.05 | 1.08 | 1.12 | 1.15 | 1.19 | 1.23 | 1.28 | 1.33 | 1.39 | 1.45 | 1.53 | 1.62 | 1.72 | 1.85 | 2.01 | 2.23 | 2.56 | 3.15 |
ハッシュ関数: うまく全体にばらまくことのできる方法が必要
→ 均等なハッシュ値を生成
「大きなデータ同士を比較する」のではなく、 「各データのハッシュ値を最初に計算しておき、ハッシュ値同士を比較して、 ハッシュ値が一致すればその時だけ元のデータ同士を比較する」
例: Unixのdiffコマンド
一方向ハッシュ関数: 元データが少し異なるとハッシュ値が大きく異なる。 ハッシュ値から元データを推測するのは困難。
例:配布するソフトウェアが改竄されていないことを保証するために、 ハッシュを計算した値を公開する.
課題提出〆切は次回の講義の開始時刻です。
| 提出先 | http://ynitta.com/class/algoA/local/handin/list.php?id=kadai12a |
|---|---|
| 提出ファイル | HashOpenAddress.java |
| コメント欄: | TestHashOpenAddress.javaにhashdata02.txtを入力として与えた時の出力 |
| Bucket.java |

|
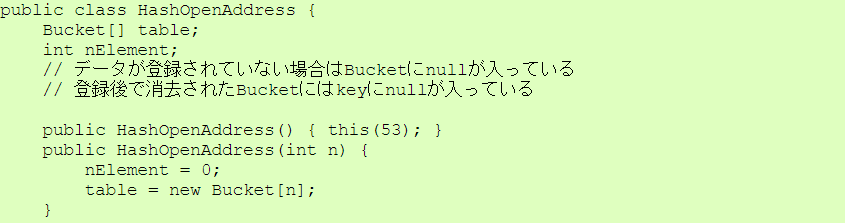
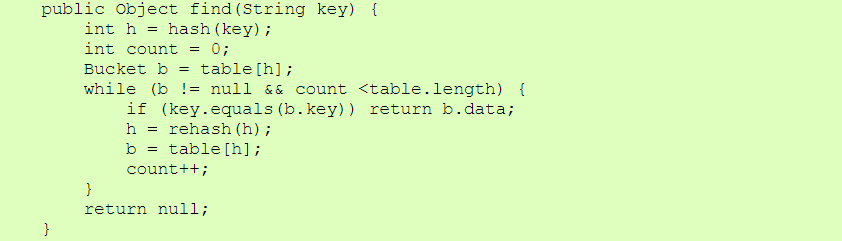
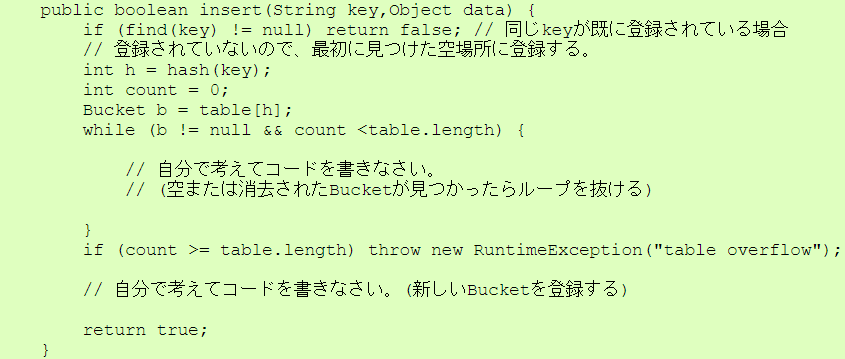
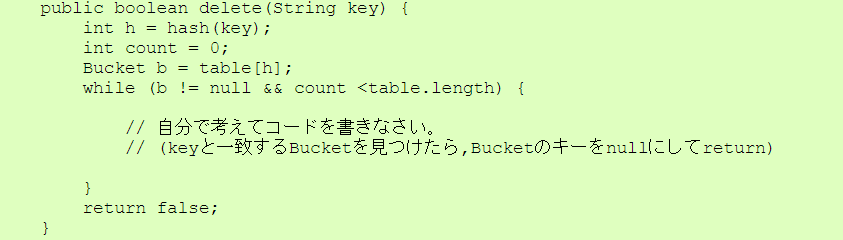
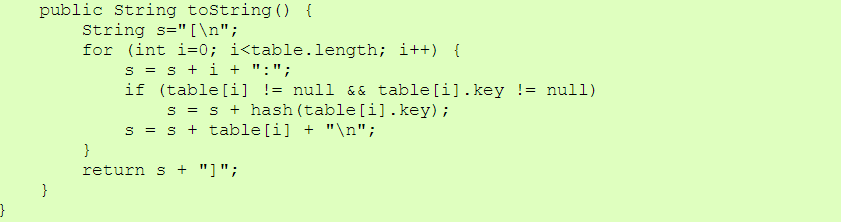
| HashOpenAddress.java |
      |
| TestHashOpenAddress.java |
  |
| hashdata01.txt |
insert a0000 89 90 68 53 insert a0008 73 80 52 69 insert a0015 70 92 55 78 insert a0017 68 73 82 82 insert a0026 53 89 82 76 insert a0027 85 72 63 68 insert a0033 85 72 63 68 show delete a0017 find a0026 find a0006 show exit |
| TestHashOpenAddress.javaの実行例 |
% javac TestHashOpenAddress.java |
| hashdata02.txt |
insert b0007 89 90 68 53 insert b0015 73 80 52 69 insert b0016 70 92 55 78 insert b0024 68 73 82 82 insert b0033 53 89 82 76 insert b0042 85 72 63 68 insert b0051 85 72 63 68 show delete b0042 find b0042 insert b0060 81 78 65 73 find b0060 show exit |
| 提出先 | http://ynitta.com/class/algoA/local/handin/list.php?id=kadai12b |
|---|---|
| 提出ファイル | HashOpenAddressRand.java |
| コメント欄: | TestHashOpenAddressRand.javaにhashdata02.txtを入力として与えた時の出力 |
ハッシュ値の再計算に、ランダム数列を用いるように変更して下さい。
| HashOpenAddressRand.javaへの変更点 |
*** java/HashOpenAddress.java Sun Sep 5 16:27:40 2021
--- java/HashOpenAddressRand.java Sun Sep 5 16:27:40 2021
***************
*** 1,13 ****
! public class HashOpenAddress {
Bucket[] table;
int nElement;
// データが登録されていない場合はBucketにnullが入っている
// 登録後で消去されたBucketにはkeyにnullが入っている
! public HashOpenAddress() { this(53); }
! public HashOpenAddress(int n) {
nElement = 0;
table = new Bucket[n];
}
private int hash(String key) {
int sum=0;
--- 1,24 ----
! import java.util.*;
! public class HashOpenAddressRand {
Bucket[] table;
int nElement;
+ int[] rt; // 再ハッシュ計算につかう表
// データが登録されていない場合はBucketにnullが入っている
// 登録後で消去されたBucketにはkeyにnullが入っている
! public HashOpenAddressRand() { this(53); }
! public HashOpenAddressRand(int n) {
nElement = 0;
table = new Bucket[n];
+ rt = new int[n]; // 再ハッシュ表の初期化
+ for (int i=0; i<n; i++) rt[i]=i;
+ Random rand = new Random(12345);
+ for (int i=1; i<n; i++) { // rt[0] should be 0
+ int j = rand.nextInt(n-1)+1;
+ int tmp = rt[i];
+ rt[i] = rt[j];
+ rt[j] = tmp;
+ }
}
private int hash(String key) {
int sum=0;
***************
*** 15,22 ****
sum += (int) key.charAt(i);
return sum % table.length;
}
! private int rehash(int h) {
! return (h+1) % table.length;
}
public Object find(String key) {
int h = hash(key);
--- 26,33 ----
sum += (int) key.charAt(i);
return sum % table.length;
}
! private int rehash(int h,int count) {
! return (h-rt[count-1]+rt[count]+table.length) % table.length;
}
public Object find(String key) {
int h = hash(key);
***************
*** 25,31 ****
while (b != null && count <table.length) {
if (key.equals(b.key)) return b.data;
count++;
! h = rehash(h);
b = table[h];
}
return null;
--- 36,42 ----
while (b != null && count <table.length) {
if (key.equals(b.key)) return b.data;
count++;
! h = rehash(h,count);
b = table[h];
}
return null;
***************
*** 39,45 ****
while (b != null && count <table.length) {
if (b.key == null) break;
count++;
! h = rehash(h);
b = table[h];
}
if (count >= table.length) throw new RuntimeException("table overflow");
--- 50,56 ----
while (b != null && count <table.length) {
if (b.key == null) break;
count++;
! h = rehash(h,count);
b = table[h];
}
if (count >= table.length) throw new RuntimeException("table overflow");
***************
*** 58,64 ****
return true;
}
count++;
! h = rehash(h);
b = table[h];
}
return false;
--- 69,75 ----
return true;
}
count++;
! h = rehash(h,count);
b = table[h];
}
return false;
|
| TestHashOpenAddressRand.javaへの変更点 |
*** java/TestHashOpenAddress.java Sun Sep 5 16:27:45 2021
--- java/TestHashOpenAddressRand.java Sun Sep 5 16:27:45 2021
***************
*** 1,5 ****
import java.util.*;
! public class TestHashOpenAddress {
static class ExamMark {
int english;
int math;
--- 1,5 ----
import java.util.*;
! public class TestHashOpenAddressRand {
static class ExamMark {
int english;
int math;
***************
*** 14,20 ****
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
! HashOpenAddress hoa = new HashOpenAddress(11);
while (sc.hasNext()) {
String line = sc.nextLine();
Scanner scLine = new Scanner(line);
--- 14,20 ----
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
! HashOpenAddressRand hoa = new HashOpenAddressRand(11);
while (sc.hasNext()) {
String line = sc.nextLine();
Scanner scLine = new Scanner(line);
|
| TestHashOpenAddressRand.javaの実行例 |
$ javac TestHashOpenAddressRand.java HashOpenAddressRand.java |