アルゴリズムa 第11回

二分木

前回学んだ「二分木」は、データを挿入する順番によってできあがる 木の状態が変わってしまいます。 探索の手間があまりかからない O(log n) 状態もあれば、 探索の手間がかかる O(n)状態もありえます。

平衡木

AVL木

教科書p.243-p.252

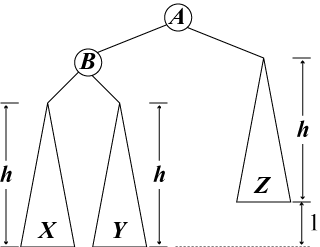
二分探索木に、

すべて節において、左部分木と右部分木の高さの差が 1 以内に収まらなければ ならない、

一重回転

1. 高さの差が1の木があったとき(図1a)
2. 部分木Xに追加されると高さの差が2になる。(図1b)
3. ノードAの親をノードBとすれば高さの差が0になる。(図1c)

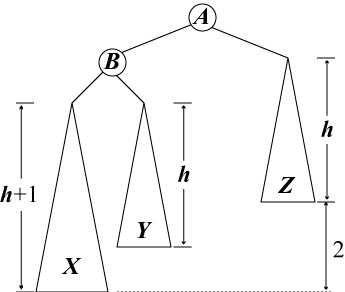
図1a	図1b	図1c

二重回転

1. 高さの差が1の木があったとき(図1a)
2. 部分木Yに追加されると高さの差が2になる。(図2b)
3. 部分木Yの中をノードCと部分木Y₁, Y₂に分解して(図2c)
4. ノードAの親をノードBとすれば高さの差が0になる。(図2d)

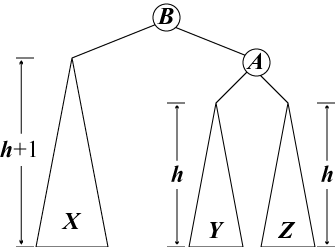
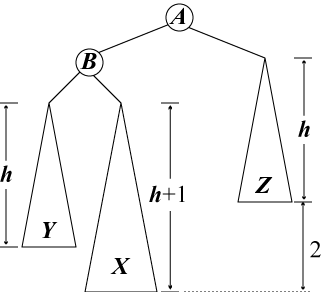
図2b	図2c	図2d

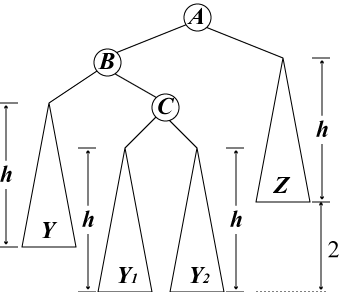
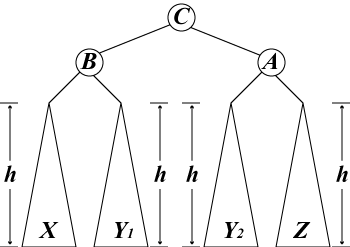
AVL木に新しい要素を挿入した時に起きる、木のバランス見直し／修正作業は、 要素を挿入した葉から根に向かって上向きに伝播していきます。(p.250 Fig.10.4)

具体的な操作の例は p.251 Fig.10.5

b木 (b-tree)

教科書p.252-p.282

「二分木」においては節は最大2個の子までしか持てませんでしたが、 「多分木(multi-way tree)」では 節が最大m個 (m≧2)の子を持つことができます(m分木)。 「多分木(multi-way tree)」を使った探索木を 「多分探索木(multi-way search tree)」と呼びます。

「B木」とはm分探索木のうち、次の条件をみたすものです。(p.254,Fig.10.6参照)

1. 根は、「葉である」か、あるいは「２〜m個の子を持つ節」である。
2. 根、葉以外の節は、ceil(m/2)〜m個の子を持つ。
3. 根からすべての葉までの経路の長さが等しい

ここで ceil(x)は「x以上で最も小さい整数」(=切り上げ)を表す。

B木では、データを保持するのは葉のみで、葉以外のノードはキーだけを保持します。 (二分探索木では、全てのノードがデータを保持していました。)

B木の構造

B木では、「葉でないNode (= 内部Node)」と 「葉」 の構造が異なります。 「内部ノードは右部分木のキーの最小値」を記録しています。 「葉」はキーと、「キーとデータの組」を交互に保持しています。

B木の探索

教科書p.255

最悪のケースは、どの節もceil(m/2) 個の子を持っている場合で、 この時のb木の高さはlog_ceil(m/2) n

最良のケースは、どの節もm個の子を持っている場合で、 この時のb木の高さは log_m n

探索の計算量は木の高さに比例しますのでo(log n) で 実行できます。

B木への挿入

教科書p.256〜p.258

データを木の適切な場所に挿入する場合に、節に保持しているデータ(子)が m個を越えるとその節を２つの節に分割します(p.257 Fig.10.7参照)。 １つの節の分割においては、m/2個のデータを新しい節にコピー しなくてはならないので、その計算量はO(m) となります。

ある節を分割した結果、その上の節も保持するデータ(子)がm個を 越えて分割しなければいけなくなる場合が起こりえます。 根まで木を遡っていくと、O(log n) 個の節を 分割することになります。

したがって、挿入の計算量は O(log n) ×O(m)ですが、 mは定数であると見なせるので、結局 O(log n) であることがわかります。

B木からの削除

教科書p.258〜p.261

あるデータ(子) L を節 α から削除するには、基本的には αの中身を詰めなおすだけで済みます(P.259,Fig.10.8(a)(b))。

しかし、その結果αの子の個数が [(m+1)/2]を下まわってしまうと、 隣りの節から要素を分けてもらう必要がでてきます。 このときαとβで子を半分ずつにします。(p.260, Fig.10.8(c))

その結果βの子の個数が[(m+1)/2]未満になる場合は、αとβを 併合します。(p.260 Fig.10.8(d))

併合の結果、上の節のデータ(子)の個数が足りなくなることがありえます。 上でも節の併合がおきると影響はさらに上へと伝播していきます。

１個の節から子を削除するときの計算量はO( m )ですが、 それが O(log n) 回起きる可能性があるので、 mは定数とみて結局削除にはO(log n)の計算量が必要で あることがわかります。

アルゴリズムa 演習

課題提出〆切は、来週の講義開始時刻です。

課題11

配列で「二分探索木」を表現することができます。 配列のインデックスを1から数えるとして、 「親ノード」のインデックスをkとすると、「左部分木の子ノード」は 2*k, 「右部分木の子ノード」は 2*k+1にすればよいのです。

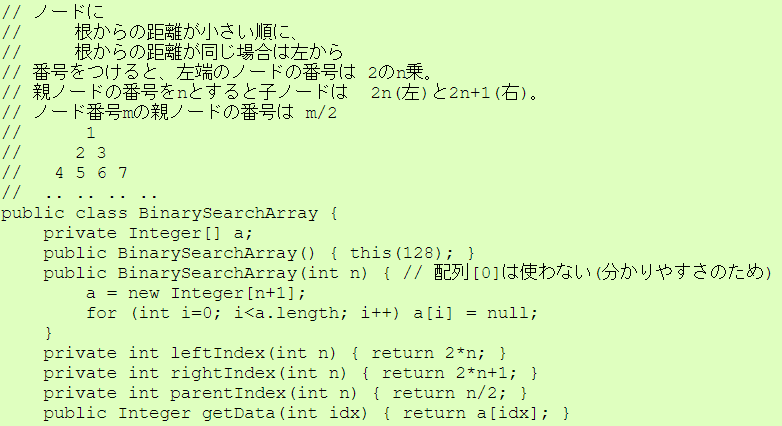
BinarySearchArray.java の欠けている部分を自分でコードを書きなさい。

BinarySearchArray.java

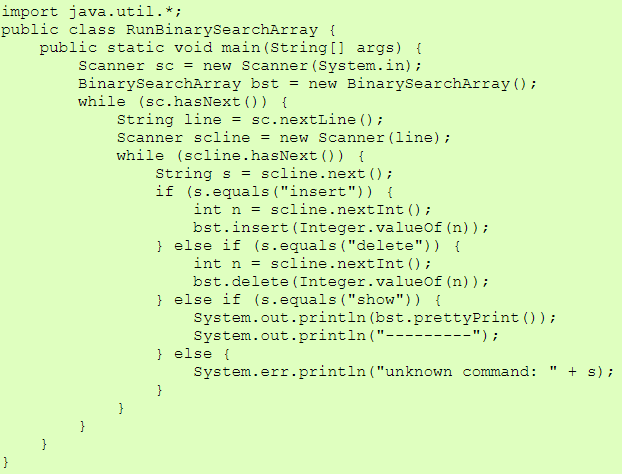
RunBinarySearchArray.java

$ javac RunBinarySearchArray.java BinarySearchArray.java   
$ java RunBinarySearchArray  <  bsearch01.txt   
      null
    15
        null
      13
        null
  11
      null
    9
      null
7
        null
      6
        null
    5
      null
  3
      null
    2
        null
      1
        null

---------
...(略)

insert 7
insert 3
insert 11
insert 5
insert 2
insert 9
insert 20
insert 13
insert 1
insert 6
insert 14
insert 16
show
delete 2
show 
delete 5
show
delete 11
show