アルゴリズムa 第10回

探索

たくさんのデータの中から、ある特定の値を持つデータを探しだす操作のこと。 探索するためには、

• 挿入 ... データを表, 木, グラフなど何らかのデータ構造に登録する
• 探索 ... 与えられた値をキーにもつデータを探し出す
• 削除 ... 与えられた値をキーにもつデータを削除する

線形探索と二分探索

この講義の第1回と第2回で学びました。

線形探索法はデータがどういう順番で並んでいても構わないのですが、 二分探索法はデータがソート済みの状態である必要がありました。

二分探索木 (Binary Search Tree)

二分木の各節にデータを持たせたもので

任意の節 x について、左部分木に含まれる要素は節xよりも小さく、 右部分木に含まれる要素は節xよりも大きい、

あるデータの集合を表す二分探索木はいくつも存在する。

        13                      6
      +--+--+                 +-+------+
      5     21                5        21
    +-+-+ +-+               +-+      +-+
    2   7 15                2        15
      +-+                          +-+
      6                            13
                                 +-+
                                 7

Javaにおいては、データが大小比較可能なオブジェクトである場合は Comparable インターフェイスを実装しており、 int compareTo(Object) メソッドを持ちます。 このメソッドの返り値は以下の意味を持ちます。

• 正 → this > 第一引数
• 0 → this == 第一引数
• 負 → this < 第一引数

2分木探索のプログラム

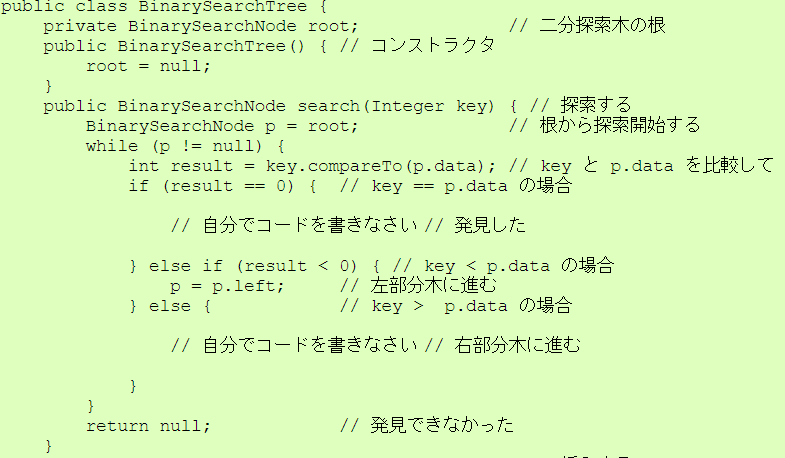
BinarySearchTreeクラスを作成し、 探索、挿入、削除に関してそれぞれ メソッドを用意すると、次のようになる。

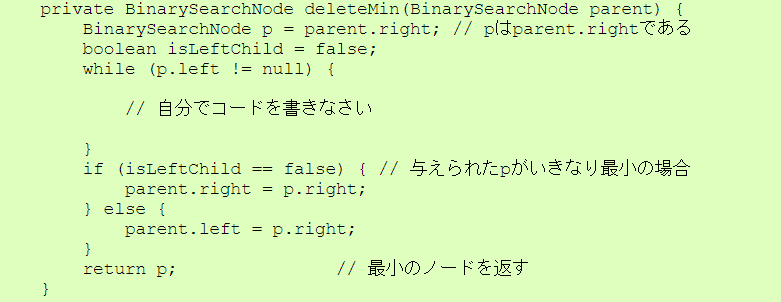
基本は「keyがノードより小さければ左部分木へ、大きければ右部分木へ」 と処理をする。 左右両方の部分木をもつノードの削除だけが少し考え方が難しいが、 「『右部分木の最小のもの』(これは、『削除するノードの次に大きいノード』 を意味する)を探してきて、削除するノードと置き換え」ればよい。 もちろん、 「『左部分木の最大のもの』(これは、『削除するノードの次に小さいノード』 を意味する)を探してきて、削除するノードと置き換え」ても構わないのだが。

BinarySearchNode.java

BinarySearchTree.java

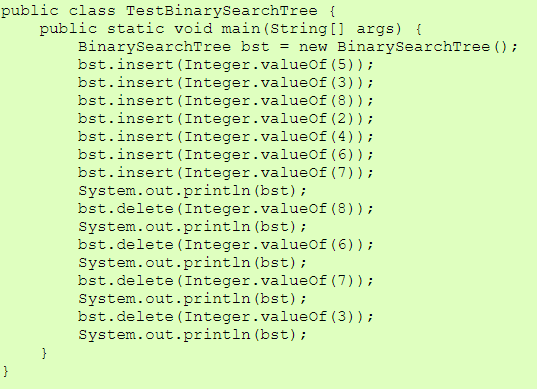
TestBinarySearchTree.java

$ javac TestBinarySearchTree.java   
$ java TestBinarySearchTree   
 2  3  4  5  6  7  8 
 2  3  4  5  6  7 
 2  3  4  5  7 
 2  3  4  5 
 2  4  5 
$ 

二分探索木においては、根から節までの経路長の平均は最良だと $O(\log n)$ となるが、最悪だと $O(n)$ になるので注意が必要である。(大きい順に、または、小さい順に挿入が起きた場合が最悪)

→平衡木 (AVL木、B Tree など) では、挿入・削除が行われるたびに 木の形を見直して、高さが log₂n 程度に収まるように 変形する。

アルゴリズムa 演習

課題提出〆切は次回の講義の開始時刻です。

課題10a

BinarySearchTree.java の欠けている部分を自分でコードを書きなさい。

課題10b

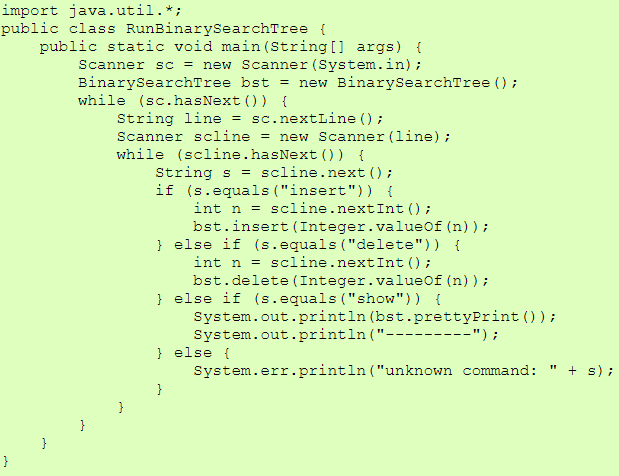
前回のサンプルプログラムのように、木構造を正しく表示する prettyPrint() メソッドを BinarySearchTree.java に追加しなさい。

RunBinarySearchTree.java

insert 7
insert 3
insert 11
insert 5
insert 2
insert 9
insert 15
insert 13
insert 1
insert 6
show
delete 2
show 
delete 5
show
delete 11
show

$ javac RunBinarySearchTree.java   
$ java RunBinarySearchTree  <  bsearch01.txt   
      null
    15
        null
      13
        null
  11
      null
    9
      null
7
        null
      6
        null
    5
      null
  3
      null
    2
        null
      1
        null

---------
...(略)