$ javac RunMyHeap.java  $ java RunMyHeap < heapdata01.txt
$ java RunMyHeap < heapdata01.txt  []
insert 7
insert 5
insert 4
insert 6
insert 2
[2 4 5 7 6 ]
insert 3
[2 4 3 7 6 5 ]
poll 2
[3 4 5 7 6 ]
poll 3
[4 6 5 7 ]
insert 1
[1 4 5 7 6 ]
poll 1
[4 6 5 7 ]
[]
insert 7
insert 5
insert 4
insert 6
insert 2
[2 4 5 7 6 ]
insert 3
[2 4 3 7 6 5 ]
poll 2
[3 4 5 7 6 ]
poll 3
[4 6 5 7 ]
insert 1
[1 4 5 7 6 ]
poll 1
[4 6 5 7 ]
ヒープを平衡木を利用して実現することも可能ですが、 それだと無駄が多いので通常は半順序木を使って実装します。
平衡木の替りに半順序木 (partial ordered tree、「親ノードは子ノードよりも小さいか等しい」 という性質を持つ木)を使う。
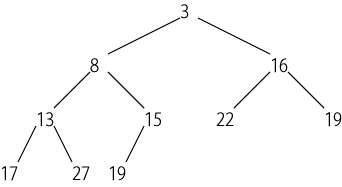
「根から葉への距離の差がどの葉に関しても1以内。最下段の葉は左に寄せる」
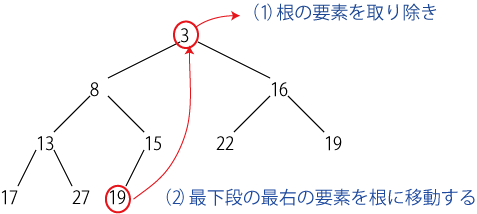
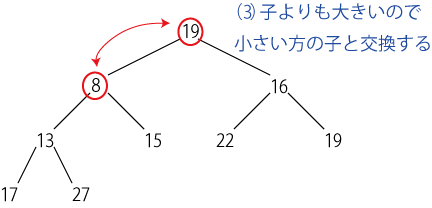



根を取り除くには、「最下段の最も右の要素」を根の場所に移動して、 あとは2つの子ノードのうち小さいものと入れ替えて行けばよい。




新しいデータを挿入するには、「最下段の最も右の要素」として挿入した後、 親ノードの方が大きい限り交換してゆく。
半順序木の実装には「ヒープ」を使う。
親ノード a[i] 子ノード a[2*i] と a[2*i+1]

| インデックス | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| データ | 未使用 | 3 | 8 | 16 | 13 | 15 | 22 | 19 | 17 | 27 | 19 | 空 | 空 | 空 | 空 | 空 |




| heapdata01.txt |
|
| RunMyHeap.javaの実行例 |
|
ヒープソートのアルゴリズム(プログラム風) p.357 List 16.1
| ヒープソートのアルゴリズム |
[1] 整列すべき配列を受け取る [2] 木を生成する [3] 木に要素を繰り返し挿入する ... O(n)回 [4] 木から最小のキーを持つ要素を取り出す操作を繰り返す ... O(n)回 |
生成する木として平衡木(AVL木やB木)や半順序木を使えば、 1個の要素を木に挿入したり、 木から削除したりする手間は O(log n)
したがって、全体の計算量は O(n log n) 。
整列すべきデータの配列の中にヒープを構築する。 p.374 Fig.16.8 のようにして半順序木を生成し、 p.373 Fig.16.6 のようにして半順序木から最も小さいデータを 配列の後ろに取り出していく。


| HeapSort.javaの実行例 |
|
作成したプログラムが正しく動作することを確認したら、それぞれの 提出先に提出しなさい。
提出した後は、正しく提出されていることを http://ynitta.com/class/algoB/local/handin/ で必ず確認しておいて下さい。
提出〆切は次回の講義の開始時刻です。
| 提出ファイル | MyHeap.java |
|---|---|
| コメント欄: | heapdata02.txtを入力として与えたときの出力 |
| 提出先: | 「宿題提出Web:アルゴリズムB:課題4a」 http://ynitta.com/class/algoB/local/handin/up.php?id=kadai4a |
MyHeap.javaの欠けている部分のコードを書きなさい。
| heapdata02.txt |
|
| 提出ファイル | HeapSort.java |
|---|---|
| コメント欄: | rand800k.txt, inc800k.txt, dec800k.txtそれぞれに対する計算時間 |
| 提出先: | 「宿題提出Web:アルゴリズムB:課題4b」 http://nw.tsuda.ac.jp/class/algoB/local/handin/up.php?id=kadai4b |
HeapSort.java が http://nw.tsuda.ac.jp/class/algoB/sortdata/ の下の 3種類のデータ
[注意] データは、右クリックで手元に保存してから使って下さい。大きいデータなのでブラウザで閲覧しようとするとブラウザの動作が停止することがあります。